Задание 711 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№711 учебника 2013-2022 (стр. 184):
Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. Для каждого из них постройте описанную окружность.
№711 учебника 2023-2024 (стр. 186):
Диагональ АС трапеции ABCD делит её на два подобных треугольника. Докажите, что АС2 = 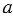

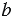 , где
, где 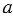 и
и 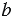 - основания трапеции.
- основания трапеции.
Подсказка
№711 учебника 2013-2022 (стр. 184):
Вспомните:
- Какой треугольник называется тупоугольным, прямоугольным, равносторонним.
- Как построить серединный перпендикуляр.
- Элементы окружности.
- Свойство вписанного прямоугольного треугольника.
№711 учебника 2023-2024 (стр. 186):
Вспомните:
- Что такое отрезок.
- Какие отрезки называются пропорциональными.
- Что такое треугольник.
- Какие треугольники называются подобными.
- Что такое трапеция.
- Что такое диагональ.
- Теорему о накрест лежащих углах.
- Признаки параллельности двух прямых.
Ответ
№711 учебника 2013-2022 (стр. 184):
1) Дано: 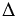 АВС - тупоугольный.
АВС - тупоугольный.
Построить: описанную около 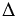 АВС окружность.
АВС окружность.
Решение:
2) Дано: 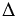 АВС - прямоугольный.
АВС - прямоугольный.
Построить: описанную около 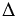 АВС окружность.
АВС окружность.
Решение:

3) Дано: 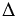 АВС - равносторонний.
АВС - равносторонний.
Построить: описанную около 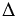 АВС окружность.
АВС окружность.
Решение:

Пояснения:
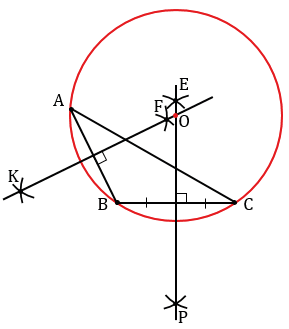
Строим тупоугольный треугольник АВС.

Центром окружности, описанной около треугольника является точка пересечения серединных перпендикуляров к сторонам данного треугольника. Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, поэтому достаточно построить серединные перпендикуляры к двум сторонам. Для того чтобы построить серединный перпендикуляр к стороне ВС, с помощью циркуля строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекутся в двух точках, обозначим их Е и Р. Далее через точки Е и Р проведем прямую ЕР, которая и будет серединным перпендикуляром к прямой ВС.

Теперь строим серединный перпендикуляр к стороне АВ. Для этого с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекутся в двух точках, обозначим их К и F. Далее через точки K и F проведем прямую KF, которая и будет серединным перпендикуляром к прямой АВ.
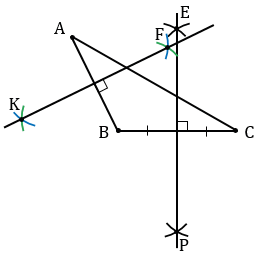
Точку пересечения серединных перпендикуляров ЕР и КF обозначаем буквой О и строим окружность с центром О радиуса ОВ, которая и будет описана около тупоугольного треугольника АВС.

2) Строим прямоугольный треугольник АВС.

В прямоугольном треугольнике один из углов прямой, т.е. равен 900, тогда дуга, на которую будет опираться данный угол, - полуокружность, т.е. равна 1800. Концы полуокружности соединяет диаметр, следовательно, у окружности, описанной около прямоугольного треугольника АВС с прямым углом В диаметром будет гипотенуза АС. Тогда для того, чтобы построить окружность около данного треугольника, нужно найти середину гипотенузы АС. Для этого с помощью циркуля строим две окружности радиуса АС с центрами в точках А и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекутся в двух точках, обозначим их К и F. Далее через точки K и F проведем прямую KF, которая будет пересекать сторону АС в ее середине - точке О.

Теперь строим окружность с центром О радиуса ОА, которая и будет описана около прямоугольного треугольника АВС.

3) Строим равносторонний треугольник АВС.
Строим серединный перпендикуляр к стороне ВС (смотри пункт 1).

Строим серединный перпендикуляр к стороне АВ (смотри пункт 1).

Точку пересечения серединных перпендикуляров АК и СР обозначаем буквой О и строим окружность с центром О радиуса ОВ, которая и будет описана около равностороннего треугольника АВС.

№711 учебника 2023-2024 (стр. 186):



Вернуться к содержанию учебника