Задание 331 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№331 учебника 2013-2022 (стр. 92):
Две стороны и угол одного треугольника равны каким-то двум сторонам и углу другого треугольника. Могут ли эти треугольники быть неравными?
№331 учебника 2023-2024 (стр. 95):
Подсказка
№331 учебника 2013-2022 (стр. 92):
Вспомните:
- Какая фигура называется треугольником.
- Какие треугольники называются равными.
- Какой треугольник называется равнобедренным.
№331 учебника 2023-2024 (стр. 95):
Вспомните:
- Что называют биссектрисой угла.
- Свойство биссектрисы угла.
- Как построить биссектрису угла.
- Какие прямые называют пересекающимися.
- Вертикальные углы.
- Расстояние от точи до прямой.
- Признаки равенства прямоугольных треугольников.
Ответ
№331 учебника 2013-2022 (стр. 92):


№331 учебника 2023-2024 (стр. 95):
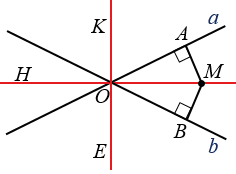
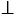 а, МВ
а, МВ 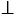 b),
b), 
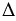 МАО =
МАО = 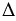 МВО по гипотенузе и катету (ОМ - общая, МА = МВ),
МВО по гипотенузе и катету (ОМ - общая, МА = МВ), 
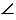 МОА =
МОА = 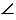 МОВ,
МОВ,  ОМ - биссектриса
ОМ - биссектриса 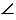 АОВ,
АОВ,  точка М лежит на биссектрисе угла, образованного при пересечении прямых а и b. Аналогично доказывается с остальными углами.
точка М лежит на биссектрисе угла, образованного при пересечении прямых а и b. Аналогично доказывается с остальными углами.Вернуться к содержанию учебника