Задание 407 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№407 учебника 2013-2022 (стр. 112):
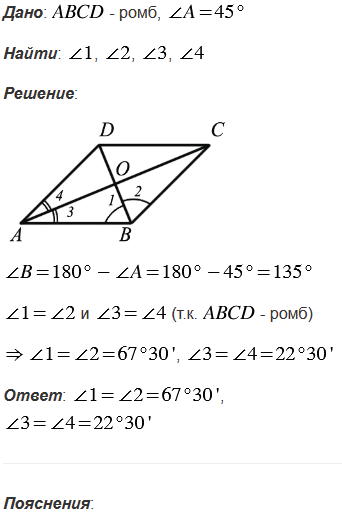
Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 450.
№407 учебника 2023-2024 (стр. 115):
Докажите, что любая прямая, проходящая через центр окружности, является её осью симметрии.
Подсказка
№407 учебника 2013-2022 (стр. 112):
Вспомните:
- Что такое параллелограмм.
- Что такое ромб.
- Теорему об односторонних углах.
№407 учебника 2023-2024 (стр. 115):
Вспомните:
- Что называют окружностью, ее элементы.
- Что называют осью симметрии фигуры.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Какие прямые называют перпендикулярными.
Ответ
№407 учебника 2013-2022 (стр. 112):

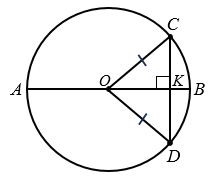
№407 учебника 2023-2024 (стр. 115):
Дано: окр. (О).
Доказать: любая прямая, проходящая через центр окружности, является её осью симметрии.
Доказательство:
Произвольно проведем прямую через центр окружности, которая пересечет окружность в точках А и В. Произвольно отметим на окружности точку С и опустим из нее перпендикуляр к прямой АВ, который пересечет окружность в точке D.
ОС = ОD - радиусы, KОD - равнобедренный с основанием KD, при этом ОК - его высота,  ОК - его медиана,
ОК - его медиана,  АВ - серединный перпендикуляр к отрезку KD,
АВ - серединный перпендикуляр к отрезку KD, 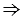 точки K и D симметричны относительно прямой АВ. Точка С выбрана произвольно,
точки K и D симметричны относительно прямой АВ. Точка С выбрана произвольно, 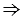 любая точки окружности симметрична какой-нибудь другой точке окружности,
любая точки окружности симметрична какой-нибудь другой точке окружности, 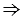 АВ - ось симметрии данной окружности. Что и требовалось доказать.
АВ - ось симметрии данной окружности. Что и требовалось доказать.
Пояснения:
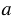 , если для каждой точки фигуры симметричная ей точка относительно прямой
, если для каждой точки фигуры симметричная ей точка относительно прямой 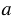 также принадлежит этой фигуре. Прямая
также принадлежит этой фигуре. Прямая 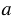 называется осью симметрии фигуры.
называется осью симметрии фигуры.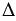 СОD. В нем стороны ОС и ОD - радиусы окружности, значит, ОС = ОD, значит,
СОD. В нем стороны ОС и ОD - радиусы окружности, значит, ОС = ОD, значит, 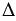 СОD - равнобедренный с основанием CD. При этом ОК - высота
СОD - равнобедренный с основанием CD. При этом ОК - высота 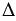 СОD, т.к. по построению СD
СОD, т.к. по построению СD 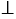 АВ. В равнобедренном треугольнике высота и медиана. проведенные к основанию совпадают, значит, ОК - еще и медиана
АВ. В равнобедренном треугольнике высота и медиана. проведенные к основанию совпадают, значит, ОК - еще и медиана 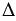 СОD, тогда СК = DK.
СОD, тогда СК = DK.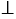 АВ и СК = DK, значит, АВ - серединный перпендикуляр к отрезку KD, следовательно, точки K и D симметричны относительно прямой АВ. Точка С выбрана нами произвольно, тогда любая точки окружности симметрична какой-нибудь другой точке окружности, значит, АВ - ось симметрии данной окружности. Что и требовалось доказать.
АВ и СК = DK, значит, АВ - серединный перпендикуляр к отрезку KD, следовательно, точки K и D симметричны относительно прямой АВ. Точка С выбрана нами произвольно, тогда любая точки окружности симметрична какой-нибудь другой точке окружности, значит, АВ - ось симметрии данной окружности. Что и требовалось доказать.Вернуться к содержанию учебника