Задание 4.203 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 43
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№4.203 учебника 2021-2022 (стр. 43):
Подберите корень уравнения и выполните проверку:
а) -3 + 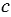 = 13;
= 13;
б) 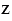 + (-4) = - 22;
+ (-4) = - 22;
в) 4 + 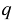 = - 20;
= - 20;
г)  + (-24) = 4.
+ (-24) = 4.
Подсказка
№4.203 учебника 2021-2022 (стр. 43):
Вспомните:
- Что такое корень уравнения.
- Сложение отрицательных чисел и чисел с разными знаками.
- Модуль числа.
Ответ
№4.203 учебника 2021-2022 (стр. 43):
а) -3 +  = 13
= 13
 = 16
= 16
Проверка:
-3 + 16 = 13
16 - 3 = 13
13 = 13.
Ответ:  = 16.
= 16.
б)  + (-4) = -22
+ (-4) = -22
 = -18
= -18
Проверка:
-18 + (-4) = -22
-(18 + 4) = -22
-22 = -22
Ответ:  = -18.
= -18.
в) 4 +  = -20
= -20
 = -24
= -24
Проверка:
4 + (-24) = -20
-(24 - 4) = -20
-20 = -20
Ответ:  = -24.
= -24.
г) 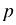 + (-24) = 4
+ (-24) = 4
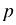 = 28
= 28
Проверка:
28 + (-24) = 4
28 - 24 = 4
4 = 4
Ответ: 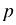 = 28.
= 28.
Пояснения:
Корень уравнения - это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
а) При подборе корня уравнения
-3 +  = 13, рассуждаем так: первое слагаемое отрицательное (-3), а сумма положительна (13), значит, второе слагаемое должно быть положительное и по модулю больше 3, т.к. чтобы сложить два числа с разными знаками, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем (обычно сначала определяют и записывают знак суммы, а потом в скобках находят разность модулей, если сумма в итоге получается положительной, то скобки можно не ставить).
= 13, рассуждаем так: первое слагаемое отрицательное (-3), а сумма положительна (13), значит, второе слагаемое должно быть положительное и по модулю больше 3, т.к. чтобы сложить два числа с разными знаками, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем (обычно сначала определяют и записывают знак суммы, а потом в скобках находят разность модулей, если сумма в итоге получается положительной, то скобки можно не ставить).
Предполагаем, что  = 16 и выполняем проверку, подставляя в уравнение число 16 вместо
= 16 и выполняем проверку, подставляя в уравнение число 16 вместо  :
:
-3 + 16 = 13,
16 - 3 = 13,
13 = 13.
Получилось верное числовое равенство, значит,  = 16 является корнем уравнения -3 +
= 16 является корнем уравнения -3 +  = 13.
= 13.
б) При подборе корня уравнения
 + (-4) = -22, рассуждаем так: второе слагаемое в уравнении отрицательное (-4), сумма также отрицательна (-22), значит, и первое слагаемое должно быть отрицательное, т.к. чтобы сложить два отрицательных числа, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); сложить модули слагаемых; перед полученным числом поставить знак " - " (обычно знак минус выносят за скобки и в скобках находят сумму модулей).
+ (-4) = -22, рассуждаем так: второе слагаемое в уравнении отрицательное (-4), сумма также отрицательна (-22), значит, и первое слагаемое должно быть отрицательное, т.к. чтобы сложить два отрицательных числа, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); сложить модули слагаемых; перед полученным числом поставить знак " - " (обычно знак минус выносят за скобки и в скобках находят сумму модулей).
Предполагаем, что  = -18 и выполняем проверку, подставляя в уравнение число -18 вместо
= -18 и выполняем проверку, подставляя в уравнение число -18 вместо  :
:
-18 + (-4) = -22,
-(18 + 4) = -22,
-22 = -22.
Получилось верное числовое равенство, значит,  = -18 является корнем уравнения
= -18 является корнем уравнения  + (-4) = -22.
+ (-4) = -22.
в) При подборе корня уравнения
4 +  = -20, рассуждаем так: первое слагаемое положительное (4), а сумма отрицательна (-20), значит, второе слагаемое должно быть отрицательное и по модулю больше 4, т.к. чтобы сложить два числа с разными знаками, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем (обычно сначала определяют и записывают знак суммы, а потом в скобках находят разность модулей, если сумма в итоге получается положительной, то скобки можно не ставить).
= -20, рассуждаем так: первое слагаемое положительное (4), а сумма отрицательна (-20), значит, второе слагаемое должно быть отрицательное и по модулю больше 4, т.к. чтобы сложить два числа с разными знаками, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем (обычно сначала определяют и записывают знак суммы, а потом в скобках находят разность модулей, если сумма в итоге получается положительной, то скобки можно не ставить).
Предполагаем, что  = -24 и выполняем проверку, подставляя в уравнение число -24 вместо
= -24 и выполняем проверку, подставляя в уравнение число -24 вместо  :
:
4 + (-24) = -20,
-(24 - 4) = -20,
-20 = -20.
Получилось верное числовое равенство, значит,  = -24 является корнем уравнения 4 +
= -24 является корнем уравнения 4 +  = -20.
= -20.
г) При подборе корня уравнения
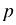 + (-24) = 4, рассуждаем так: второе слагаемое отрицательное (-24), а сумма положительна (4), значит, второе слагаемое должно быть положительное и по модулю больше 24, т.к. чтобы сложить два числа с разными знаками, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем (обычно сначала определяют и записывают знак суммы, а потом в скобках находят разность модулей, если сумма в итоге получается положительной, то скобки можно не ставить).
+ (-24) = 4, рассуждаем так: второе слагаемое отрицательное (-24), а сумма положительна (4), значит, второе слагаемое должно быть положительное и по модулю больше 24, т.к. чтобы сложить два числа с разными знаками, надо: найти модули слагаемых (модуль числа принимает только неотрицательные значения); из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем (обычно сначала определяют и записывают знак суммы, а потом в скобках находят разность модулей, если сумма в итоге получается положительной, то скобки можно не ставить).
Предполагаем, что 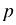 = 28 и выполняем проверку, подставляя в уравнение число 28 вместо
= 28 и выполняем проверку, подставляя в уравнение число 28 вместо 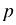 :
:
28 + (-24) = 4,
28 - 24 = 4,
4 = 4.
Получилось верное числовое равенство, значит, 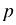 = 28 является корнем уравнения
= 28 является корнем уравнения 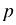 + (-24) = 4.
+ (-24) = 4.
Вернуться к содержанию учебника