Упражнение 139 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№139 учебника 2023-2025 (стр. 34):
Имеет ли уравнение корни и, если имеет, то сколько:
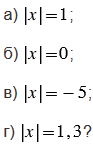
№139 учебника 2013-2022 (стр. 31):
Укажите все целые значения \(y\), при которых верно двойное неравенство:
а) \(-5 < y < 2\);
б) \(28 \le y \le 31{,}2\).
Подсказка
№139 учебника 2023-2025 (стр. 34):
Вспомните:
- Что называют корнем уравнения.
- Модуль числа.
- Положительные и отрицательные числа (противоположные числа).
№139 учебника 2013-2022 (стр. 31):
Вспомните, какие числа называют целыми.
Ответ
№139 учебника 2023-2025 (стр. 34):

Пояснения:
Модуль числа принимает только неотрицательные значения, поэтому уравнение из пункта в) не имеет корней.
Модули противоположных чисел равны, поэтому уравнения из пунктов а) и г) имеют 2 корня, а уравнение из пункта б) имеет 1 корень, так как ноль противоположен сам себе.
№139 учебника 2013-2022 (стр. 31):
а) \(y =-4; -3; -2; -1; 0; 1\).
б) \(y =28; 29; 30; 31\).
Пояснения:
1) Правило двойного неравенства.
\[a < y < b\] означает одновременное выполнение двух условий: \(y > a\) и \(y < b\).
\[a \le y \le b\] означает одновременное выполнение условий: \(y \ge a\) и \(y \le b\).
2) Поиск целых значений.
Целые \(y\) выбираются от первого целого, строго большего левой границы, до последнего целого, строго меньшего (или не превосходящего) правой границы.
– В пункте а) левая граница \(-5\), первая целая > \(-5\) — это \(-4\); правая граница \(2\), последнее целое < 2 — это 1; перечисляем \(-4, -3, -2, -1, 0, 1\).
– В пункте б) левая граница 28 включена, правая граница 31,2 не включена целыми числами, поэтому целые \(y\) от 28 до 31 включительно: 28, 29, 30, 31.
Вернуться к содержанию учебника