Упражнение 290 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№290 учебника 2023-2025 (стр. 66):
(Для работы в парах.) На рисунке 29 изображены графики зависимости высоты уровня жидкости от ее объема в двух сосудах различной формы, но одной и той же емкости - 3 л. Пользуясь графиками, найдите:
а) какое количество жидкости надо налить в каждый сосуд, чтобы уровень жидкости в них был одинаков;
б) сколько жидкости надо налить во второй сосуд, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости.

Рис. 29
1) Распределите, кто выполнит задание а), а кто - задание б), и выполните их.
2) Объясните друг другу, как вы рассуждали при выполнении задания, и изобразите схематически, какую примерно форму имеют эти сосуды.
№290 учебника 2013-2022 (стр. 67):
(Для работы в парах.) На рисунке 19 изображены графики зависимости высоты уровня жидкости от ее объема в двух сосудах различной формы, но одной и той же емкости - 3 л. Пользуясь графиками, найдите:
а) какое количество жидкости надо налить в каждый сосуд, чтобы уровень жидкости в них был одинаков;
б) сколько жидкости надо налить во второй сосуд, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости.

Рис. 19
1) Распределите, кто выполнит задание а), а кто - задание б), и выполните их.
2) Объясните друг другу, как вы рассуждали при выполнении задания, и изобразите схематически, какую примерно форму имеют эти сосуды.
Подсказка
№290 учебника 2023-2025 (стр. 66):
№290 учебника 2013-2022 (стр. 67):
Вспомните:
Ответ
№290 учебника 2023-2025 (стр. 66):
№290 учебника 2013-2022 (стр. 67):
1) а) В каждый сосуд нужно налить 2,5 л, чтобы уровень жидкости в них был одинаков -100 мм.
б) Во второй сосуд надо налить 1,875 л, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости - 60 мм.
2)

Пояснения:
Объяснение друг другу:
а) Уровень жидкости в сосудах одинаков в точке пересечения графиков. Графики пересекаются в точке с координатами (2,5; 100), значит, в каждый сосуд нужно налить 2,5 л, чтобы уровень жидкости в них был одинаков - 100 мм.

б) Чтобы узнать, сколько жидкости надо налить во второй сосуд, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости, сначала нужно определить высоту уровня жидкости в первом сосуде, соответствующую объему 1,5 л. Для этого через точку на оси объема 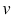 , равную 1,5, надо провести перпендикуляр, этот перпендикуляр пересечет график в точке с координатами (1,5; 60). Значит, при
, равную 1,5, надо провести перпендикуляр, этот перпендикуляр пересечет график в точке с координатами (1,5; 60). Значит, при 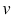 = 1,5 л высота жидкости в первом сосуде
= 1,5 л высота жидкости в первом сосуде  = 60 мм. Затем через значение 60 на оси
= 60 мм. Затем через значение 60 на оси  нужно провести прямую, параллельную оси
нужно провести прямую, параллельную оси 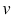 , которая пересечет график 2-го сосуда в точке с координатами (60; 1875). Значит, при
, которая пересечет график 2-го сосуда в точке с координатами (60; 1875). Значит, при  = 60 мм, объем жидкости во втором сосуде
= 60 мм, объем жидкости во втором сосуде 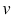 = 1,875 л. Следовательно, во второй сосуд надо налить 1,875 л, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости.
= 1,875 л. Следовательно, во второй сосуд надо налить 1,875 л, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости.

При определении значений объема учитываем то, что по оси объема 4 клетки тетради соответствуют объему 0,5 л, тогда одна клетка соответствует объему 0,5 : 4 = 0,125 (л)
| - | 0 | 5 | 4 | |||||||||||||
| 4 | 0 | 1 | 2 | 5 | ||||||||||||
| - | 1 | 0 | ||||||||||||||
| 8 | ||||||||||||||||
| - | 2 | 0 | ||||||||||||||
| 2 | 0 | |||||||||||||||
| 0 |
По графику 1-го сосуда видим, что при увеличении объема высота жидкости увеличивается равномерно, значит, диаметр сосуда постоянный и он имеет форму цилиндра.
По графику 2-го сосуда видим, что при увеличении объема сначала высота жидкости увеличивается медленнее, чем у первого сосуда, а затем - быстрее, значит, сначала диаметр второго сосуда больше диаметра первого сосуда, а затем сосуд сужается и его диаметр становится меньше диаметра первого сосуда.

Вернуться к содержанию учебника