Упражнение 1220 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

M\((x; y)\)

\(x = 2\), \(y = 3\), значит, M\((2; 3)\).

A\(\bigl(2x; 2y\bigr)\)

\(2x = 2\cdot2 = 4\),

\(2y = 2\cdot3 = 6\), значит, A\((4; 6)\).

B\(\bigl(-3x; \tfrac12y\bigr)\)

\(-3x = -3\cdot2 = -6\),

\(\tfrac12y =\tfrac12\cdot3 = \tfrac32 =1,5\),

значит, B\((-6; 1,5)\).

C\(\bigl(\tfrac12x; -2y\bigr)\)

\(\tfrac12x = \tfrac12\cdot2 = 1\),

\(-2y = -2\cdot3 = -6\), значит, С\((1; -6)\).

D\(\bigl(-\tfrac12x,-\tfrac13y\bigr)\)

\(-\tfrac12x = -\tfrac12\cdot2 = -1\),

\(-\tfrac13y = -\tfrac13\cdot3 = -1\), значит, D\((-1; -1)\).

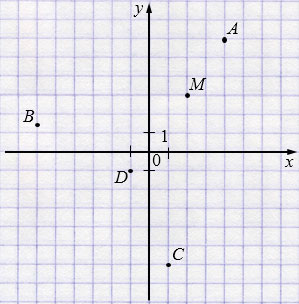
Пояснения:

1. Точка M имеет координаты \((x,y)\).

2. Координаты новых точек получаются так:

– A: умножаем обе координаты M на 2 → \(\bigl(2x,2y\bigr)\).

– B: абсциссу умножаем на –3, ординату на ½ → \(\bigl(-3x,\tfrac12y\bigr)\).

– C: абсциссу делим на 2, ординату умножаем на –2 → \(\bigl(\tfrac12x,-2y\bigr)\).

– D: абсциссу меняем знак и делим на 2, ординату меняем знак и делим на 3 → \(\bigl(-\tfrac12x,-\tfrac13y\bigr)\).

\( 3x = 23 - 7y \)

\(x = \frac{23 - 7y}{3}. \)

Числитель \(23 - 7y > 0\), так как \(x\) - натуральное число и должен делиться на 3.

Если \(y=1\), то

\(23 -7\cdot1 =16\), не делится на 3;

Если \(y=2\), то

\(23 -7\cdot2 =9\), делится на 3, тогда

\(x=\frac93=3\);

Если \(y = 3\), то

\(23 -7\cdot3 =2\) - не делится на 3.

Если \(y>3\), то \(x < 0\).

Ответ: при \(\;y=2,\;x=3.\)

Пояснения:

1) Из уравнения \(3x+7y=23\) выражаем \(x\), для этого вычитаем \(7y\) и делим на 3.

2) Натуральность \(x\) требует, чтобы числитель \(23-7y\) был положительным числом и делился нацело на 3.

3) Подстановка показывает, что при \(y=2\) получается единственное натуральное \(x=3\).