Упражнение 1003 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

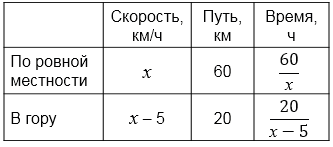
На весь путь - \(6\) ч.

Составим равнение:

\( \frac{20}{x-5}+\frac{60}{x}=6 \) \(/\times x(x-5)\)

ОДЗ: \(x - 5 > 0\)

          \(x > 5\)

\( 20x+60(x-5)=6x(x-5)\)

\(20x + 60x - 300 = 6x^2 -30x\)

\(80x-300=6x^2-30x \)

\(6x^2 - 30x - 80 x + 300 = 0\)

\(6x^2-110x+300=0 \)    \(/ : 2\)

\( 3x^2-55x+150=0\)

\(a = 3\),  \(b = -55\),  \(c = 150\)

\(D = b^2 - 4ac=\)

\( =55^2-4\cdot3\cdot150=1225 \)

\(\sqrt D = 35\)

\( x_{1,2}=\frac{-b + \sqrt D}{2a}\)

\(x_1 = \frac{-(-55)+35}{2\cdot3}=\frac{90}{6} = 15\).

\(x_2 = \frac{-(-55)-35}{2\cdot3}=\frac{20}{6} =\)

\(=\frac{10}{3} = 3\frac13\) - не удовлетворяет условию.

1) \(15\) (км/ч) - скорость по ровной местности.

2) \(15 - 5 = 10\) (км/ч) - скорость в гору.

Ответ: по ровной местности скорость равна \(15\) км/ч, в гору — \(10\) км/ч.

Пояснения:

Использовали формулу времени:

\(\;t=\dfrac{s}{v}\),

где \(t\) - время, \(s\) - расстояние (путь), \(v\) - скорость.

Общее время — сумма времен на каждом участке..

Составили уравнение дробное рациональное уравнение, учитывая то, что общее время равно сумме времен на каждом участке:

\(\dfrac{20}{x-5}+\dfrac{60}{x}=6\).

Алгоритм решения дробного рационального уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили полное квадратное уравнение

\( 3x^2-55x+150=0\), у которого дискриминант больше нуля, следовательно, имеем два корня уравнения:

\(x_1 = 15\) и \(x_2 = 3\frac13\),

но второй корень не подходит, так как \(3\frac13<5\) и в таком случае скорость в гору будет отрицательной.

Значит, скорость по ровной местности будет равна \(15\) км/ч, а скорость в гору \(15 - 5 = 10\) (км/ч).

а) \( (6a^{-5}b)^{-1} = 6^{-1} (a^{-5})^{-1}b^{-1} = \)

\(=\dfrac{1}{6}a^{5}b^{-1}. \)

б) \( \left(\dfrac{3}{4}a^{-1}b^{-3}\right)^{-2} =\)

\(=\left(\dfrac{3}{4}\right)^{-2} (a^{-1})^{-2}(b^{-3})^{-2} =\)

\(=\left(\dfrac{4}{3}\right)^{2}a^{2}b^{6} = \dfrac{16}{9}a^{2}b^{6}=1\dfrac{7}{9}a^{2}b^{6}. \)

в) \( (-0{,}3x^{-5}y^{4})^{-2} =\)

\(=(-\frac{3}{10})^{-2}(x^{-5})^{-2}(y^{4})^{-2} =\)

\(=( -\frac{10}{3})^{2}x^{10}y^{-8} = \dfrac{100}{9}x^{10}y^{-8} =\)

\(=11\dfrac{1}{9}x^{10}y^{-8} .\)

г) \( \left(\dfrac{7}{8}p^{-6}q\right)^{-1} =\)

\(=\left(\dfrac{7}{8}\right)^{-1} (p^{-6})^{-1}q^{-1} =\)

\(=\dfrac{8}{7}p^{6}q^{-1} = 1\dfrac{1}{7}p^{6}q^{-1}. \)

Пояснения:

Используемые свойства степеней:

\( (ab)^{n} = a^{n}b^{n}, \)

\((a^{m})^{n} = a^{m \cdot n},\)

\((\frac ab)^{-n} = (\frac ba)^{n} = \frac{b^n}{a^n},\)

\(a^{-n} = \dfrac{1}{a^{n}}. \)