Многоугольники. Правильные многоугольники. Равенство фигур.

Многоугольник - замкнутая ломаная, несмежные звенья которой не имеют общих точек, звенья ломаной - стороны многоугольника, а длина ломаной - периметр многоугольника. Другими словами, периметр  многоугольника - это сумма длин всех его сторон.

Любой многоугольник имеет следующие элементы: вершины, стороны и углы. Например, на рис. 1 у четырехугольника АВСD  точки А, В, С, D  являются его вершинами, отрезки АВ, ВС, СD, DА - его сторонами, углы А, В, С, D  - углами четырёхугольника.

Многоугольник с n вершинами называется n-угольником; он имеет n сторон. На рис.1 изображены четырехугольник АВСD и шестиугольник А₁А₂А₃А₄А₅А₆. Также примером многоугольника является треугольник.

Соседние вершины многоугольника - вершины, принадлежащие одной стороне. На рис.1 у четырехугольника АВСD соседние вершины: А и В, В и С, С и D, А и D.

Диагональ многоугольника - отрезок, соединяющий любые две несоседние вершины. На рис.2 отрезки АС и ВD - диагонали четырехугольника АВСD.

Выпуклый многоугольник - это многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. На рис.3 многоугольник М₁ является выпуклым многоугольником, а многоугольник М₂ - невыпуклым.

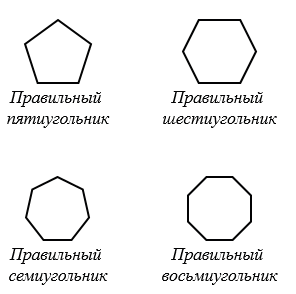
Правильный многоугольник - это выпуклый многоугольник, у которого все углы равны и все стороны равны. К правильным многоугольникам относятся равносторонний треугольник и квадрат. На рисунке ниже изображены правильные пятиугольник, шестиугольник, семиугольник и восьмиугольник.

Равными фигурами считаются те, которые имеют одинаковую форму и размеры. Две фигуры (в том числе и многоугольники) называются равными, если их можно совместить наложением. Например, пятиугольник ABCDF равен пятиугольнику A₁B₁C₁D₁F₁:

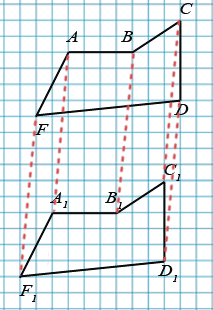
Действительно данные пятиугольники равны, они совпадут при наложении, так как вершина A совместиться с вершиной А₁, В - с В₁, C - с C₁, D - с D₁, F - с F₁.