Номер 301 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 73
Вернуться к содержанию учебника
Упражнения § 9. Страница 73
Вопрос
Порядок числа 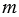 равен 2, а порядок числа
равен 2, а порядок числа 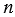 равен 4. Каким может быть порядок значения выражения:
равен 4. Каким может быть порядок значения выражения:

Подсказка
Вспомните:
- Степень с целым показателем, стандартный вид числа.
- Свойства степени с целым показателем.
- Сложение рациональных чисел.
- Десятичная запись дробных чисел.
- Распределительное свойство умножения.
- Разложение многочленов на множители.
Ответ

Ответ: порядок значения выражения 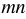 может быть равен 6 или 7.
может быть равен 6 или 7.

Ответ: порядок значения выражения 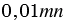 может быть равен 4 или 5.
может быть равен 4 или 5.
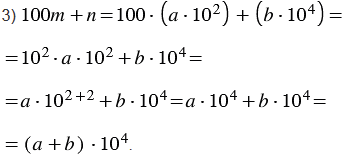
Ответ: порядок значения выражения  может быть равен 4 или 5.
может быть равен 4 или 5.
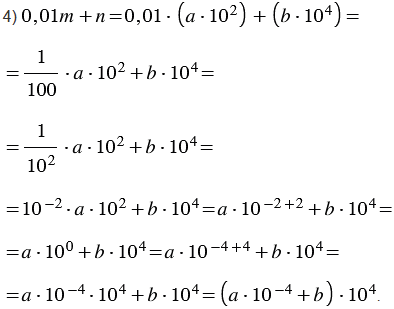
Ответ: порядок значения выражения  может быть равен 4 или 5.
может быть равен 4 или 5.
Пояснения:
Стандартным видом числа называют его запись в виде произведения  , где
, где 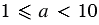 и
и 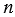 - целое число. Число
- целое число. Число 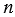 называют порядком числа, записанного в стандартном виде
называют порядком числа, записанного в стандартном виде  .
.
Для любого числа  , не равного нулю, и натурального числа
, не равного нулю, и натурального числа 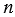 справедливо равенство:
справедливо равенство: 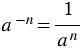 .
.
Также помним следующее свойство степени: для любого 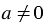 и любых целых
и любых целых  и
и 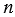 выполняются равенства:
выполняются равенства:  .
.
По условию порядок числа  равен 2, а порядок числа
равен 2, а порядок числа 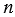 равен 4, значит,
равен 4, значит, 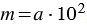 , где
, где 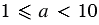 и
и 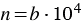 , где
, где  .
.
Рассмотрим подробное решение задания из первого пункта.
Определим, каким может быть порядок значения выражения 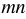 .
.
Учитывая то, что 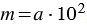 и
и 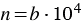 , получаем:
, получаем:

Сгруппируем множители в рассматриваемом произведении так как указано ниже, при этом учитываем свойство умножения степеней с одинаковыми основаниями:
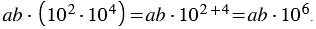
При записи выражения  в стандартном виде должно выполняться условие
в стандартном виде должно выполняться условие 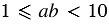 , но по условию
, но по условию 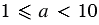 и
и  , значит, может получится так, что
, значит, может получится так, что 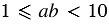 или
или 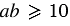 , тогда:
, тогда:
- число
 будет иметь порядок 6, если
будет иметь порядок 6, если 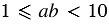 ;
; - число
 будет иметь порядок 7, если
будет иметь порядок 7, если 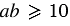 .
.
Итак, получается, порядок значения выражения 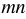 может быть равен 6 или 7.
может быть равен 6 или 7.
Рассмотрим подробное решение задания из второго пункта.
Определим, каким может быть порядок значения выражения 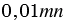 .
.
Учитывая то, что 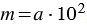 и
и 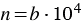 и то, что
и то, что  получаем:
получаем:

Сгруппируем множители в рассматриваемом произведении так как указано ниже, при этом учитываем свойство умножения степеней с одинаковыми основаниями:
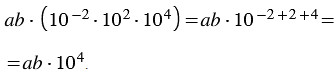
При записи выражения 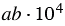 в стандартном виде должно выполняться условие
в стандартном виде должно выполняться условие 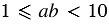 , но по условию
, но по условию 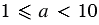 и
и  , значит, может получится так, что
, значит, может получится так, что 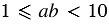 или
или 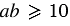 , тогда:
, тогда:
- число
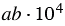 будет иметь порядок 4, если
будет иметь порядок 4, если 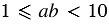 ;
; - число
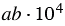 будет иметь порядок 5, если
будет иметь порядок 5, если 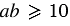 .
.
Итак, получается, порядок значения выражения 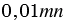 может быть равен 4 или 5.
может быть равен 4 или 5.
Рассмотрим подробное решение задания из третьего пункта.
Определим, каким может быть порядок значения выражения  .
.
Учитывая то, что 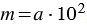 и
и 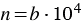 и то, что 100 = 102 получаем:
и то, что 100 = 102 получаем:
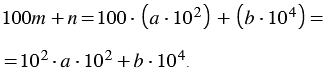
Учитывая свойство умножения степеней с одинаковыми основаниями, 102102 = 102+2 = 104, получаем следующее выражение:
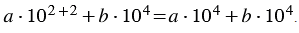
В полученном выражении выносим за скобки общий множитель 104, получаем:
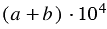 .
.
При записи выражения 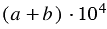 в стандартном виде должно выполняться условие
в стандартном виде должно выполняться условие  , но по условию
, но по условию 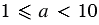 и
и  , значит, может получится так, что
, значит, может получится так, что  или
или  , тогда:
, тогда:
- число
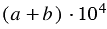 будет иметь порядок 4, если
будет иметь порядок 4, если  ;
; - число
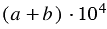 будет иметь порядок 5, если
будет иметь порядок 5, если  .
.
Итак, получается, порядок значения выражения  может быть равен 4 или 5.
может быть равен 4 или 5.
Рассмотрим подробное решение задания из четвертого пункта.
Определим, каким может быть порядок значения выражения  .
.
Учитывая то, что 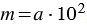 и
и 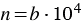 и то, что
и то, что  получаем:
получаем:

Учитывая свойство умножения степеней с одинаковыми основаниями, 10-2102 = 10-2+2 = 100 = 10-4+4 = 10-4104, получаем следующее выражение:
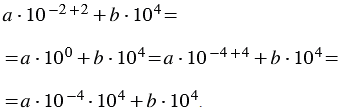
В полученном выражении выносим за скобки общий множитель 104, получаем:
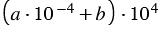 .
.
При записи выражения 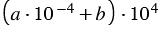 в стандартном виде должно выполняться условие
в стандартном виде должно выполняться условие 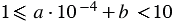 , но по условию
, но по условию 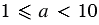 и
и  , значит, может получится так, что
, значит, может получится так, что 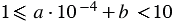 или
или  , тогда:
, тогда:
- число
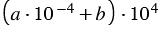 будет иметь порядок 4, если
будет иметь порядок 4, если 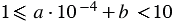 ;
; - число
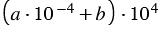 будет иметь порядок 5, если
будет иметь порядок 5, если  .
.
Итак, получается, порядок значения выражения  может быть равен 4 или 5.
может быть равен 4 или 5.
Вернуться к содержанию учебника