Упражнение 190 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№190 учебника 2023-2025 (стр. 44):
Подсчитать приближенно пройденное человеком расстояние можно, используя формулу 
, где 
- пройденное расстояние в метрах, 
- число шагов,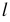 
- длина шага. Сколько километров прошел человек, если длина его шага 60 см, а сделал он 1800 шагов?
№190 учебника 2013-2022 (стр. 45):
В таблице показано, сколько акций одинаковой стоимости некоторого акционерного общества приобрели сотрудники отдела:
| № п/п | Фамилия | Число акций |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Астахова Бодров Волков Ерин Ильин Куликова Лаврова Михайлов Муравьев Николаева Осипов Павлов Петров Райков Тимофеев Фёдоров |
5 4 10 3 2 10 25 3 1 4 12 6 8 10 2 4 |
Найдите медиану этого ряда данных. У кого из сотрудников отдела число приобретённых акций не превосходит медиану?
Подсказка
№190 учебника 2023-2025 (стр. 44):
Вспомните:
- Вычисления по формулам.
- Умножение на числа, оканчивающихся нулями.
- Единицы измерения длины.
№190 учебника 2013-2022 (стр. 45):
Вспомните:
- Что называют медианой числового ряда.
- Как найти среднее арифметическое двух чисел.
- Деление десятичных дробей.
Ответ
№190 учебника 2023-2025 (стр. 44):
= 1800,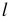 
= 60 см,
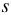= 1800 • 60 = 108 000 см = 1080 м =
= 1,08 км
| × | 1 | 8 | 0 | ||
| 6 | 0 | 0 | |||
| 1 | 0 | 8 | 0 | 0 | 0 |
Ответ: 1,08 км прошел человек.
Пояснения:
В формулу вместо известных переменных подставляем числовые значения, им соответствующие, и, выполнив вычисления, находим неизвестную переменную.
№190 учебника 2013-2022 (стр. 45):
Упорядочим значения по возрастанию:
1, 2, 2, 3, 3, 4, 4, 4, 5, 6, 8, 10, 10, 10, 12, 25.
Медиана:
\(\displaystyle \frac{4 + 5}{2} = 4{,}5.\)
Сотрудники с числом акций ≤ 4,5 (то есть ≤ 4):
Муравьёв (1), Ильин (2), Тимофеев (2), Ерин (3), Михайлов (3), Бодров (4), Николаева (4), Фёдоров (4).
Пояснения:
1) Медиана — значение, делящее упорядоченный ряд на две равные по числу элементов части; при чётном числе элементов это среднее двух центральных.
2) Чтобы определить, у кого число акций не превосходит медиану, выбираем всех сотрудников, у которых значение ≤ медианы.
Вернуться к содержанию учебника