стр. 202. Контрольные вопросы и задания - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

1) Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.

Объединением множеств называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.

2) 1. Числовой отрезок

\([a;b]\)

2. Интервал

\((a; b)\)

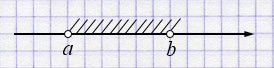
3. Полуинтервал

\([a; b)\)

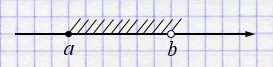
4. Полуинтервал

\((a; b]\)

5. Числовой луч

\([a; +\infty)\)

6. Числовой луч

\((-\infty; a]\)

7. Открытый числовой луч

\((a; +\infty)\)

8. Открытый числовой луч

\((-\infty; a)\)

3) Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.

\(3x-11>1\)

1) \(x = 5\) - является решением неравенства.

\(3\cdot5-11>1\)

\(15-11>1\)

\(4 > 1\) - верно.

2) \(x = 2\) - не является решением неравенства.

\(3\cdot2-11>1\)

\(6-11>1\)

\(-5 > 1\) - неверно.

Решить неравенство - значит найти все его решения или доказать, что решений нет.

4) Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

\[ \begin{cases} 2x+1>3,\\ 3x<10 \end{cases} \]

1) \(x = 3\) - является решением системы.

\[ \begin{cases} 2\cdot3+1>3,\\ 3\cdot3<10 \end{cases} \]

\[ \begin{cases} 6+1>3,\\ 9<10 \end{cases} \]

\[ \begin{cases} 7>3 - верно,\\ 9<10 - верно. \end{cases} \]

2) \(x = 5\) - не является решением системы.

\[ \begin{cases} 2\cdot5+1>3,\\ 3\cdot5<10 \end{cases} \]

\[ \begin{cases} 10+1>3,\\ 15<10 \end{cases} \]

\[ \begin{cases} 11>3 - верно,\\ 9<10 - неверно. \end{cases} \]

Решить систему неравенств - значит найти все ее решения или доказать, что решений нет.