Упражнение 106 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 36
Вернуться к содержанию учебника
Вопрос
Известно, что функция \(y = f(x)\), заданная на отрезке, симметричном, относительно начала координат, является четной. На рисунке 14, а, б изображена только часть ее графика. Достройте график этой функции, перечертив рисунок в тетрадь.
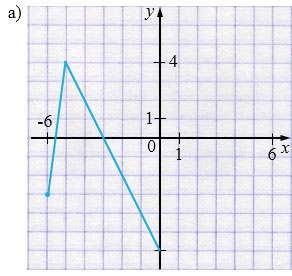
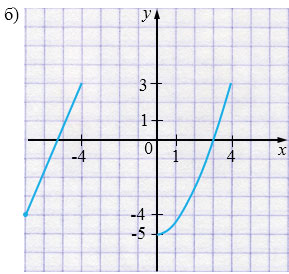
Рис. 14
Подсказка
Вспомните:
- Какую функцию называют четной.
- График функции.
- Координатную плоскость.
Ответ
а) \(y=f(x)\) - четная функция.
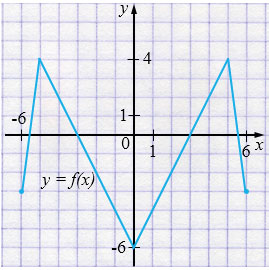
б) \(y=f(x)\) - нечетная функция.
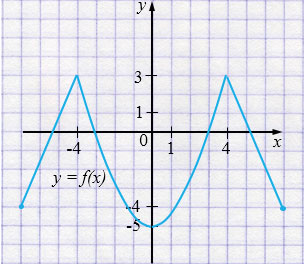
Пояснения:
Функция называется четной, если выполняются следующие условия:
- область определения функции симметрична относительно оси ординат (оси \(y)\);
- противоположным значениям аргумента соответствуют равные значения функции.
Следовательно, функция \(y = f(x)\) является четной, если для любых значений \(x\) из области определения функции справедливо равенство \(f(-x) = f(x) \).
Вернуться к содержанию учебника