Упражнение 120 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 48
Вернуться к содержанию учебника
Вопрос
Постройте в одной системе координат графики функций \[ y = x^{2}, y = 1{,}8x^{2},y = \frac{1}{3}x^{2}. \] Сравните значения этих функций при \(x = 0,5\), \(x = 1\) и \(x = 2\).
Подсказка
Ответ
\(y = x^{2}\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
\(y = 1{,}8x^{2}\)
| \(x\) | -2,5 | -2 | -1,5 | -1 |
| \(y\) | 11,25 | 7,2 | 4,05 | 1,8 |
| \(x\) | 0 | 1 | 1,5 | 2 | 2,5 |
| \(y\) | 0 | 1,8 | 4,05 | 7,2 | 11,25 |
\(y = \frac{1}{3}x^{2}\)
| \(x\) | -6 | -3 | 0 | 3 | 6 |
| \(y\) | 12 | 3 | 0 | 3 | 12 |
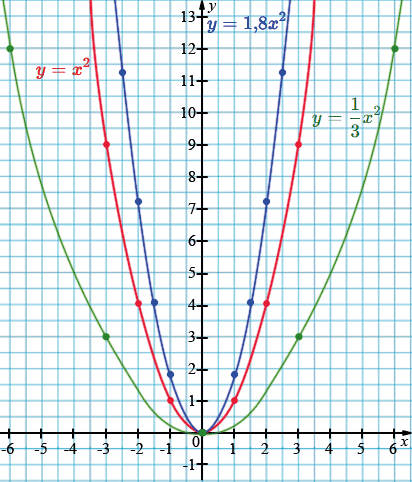
Найдём значения функций по графику.
| \(x\) | 0,5 | 1 | 2 |
| \(y = x^{2}\) | 0,25 | 1 | 4 |
| \(y = 1{,}8x^{2}\) | 0,5 | 1,8 | 7,2 |
| \(y = \frac{1}{3}x^{2}\) | 0,1 | 0,3 | 1,3 |
Сравнение значений:
Во всех трёх случаях выполняется:
\( 1,8x^{2} > x^{2} > \frac{1}{3}x^{2}. \)
Пояснения:
1. Все три функции имеют вид \(y = kx^{2}\).
Графики — параболы с вершиной в точке (0;0). Параметр \(k\) определяет «ширину» и «крутизну» параболы:
\( k = 1,8\) (самая узкая, растёт быстрее всех)
\( k = 1\) (обычная парабола)
\( k = \frac{1}{3}\) (самая широкая, растёт медленнее всех).
2. Подстановка значений.
Для каждого значения \(x\) подставляем его в формулы, сначала возводим в квадрат, затем умножаем на коэффициент.
3. Сравнение функций.
Так как квадраты для всех функций имеют одно и то же значение, то различие — только в коэффициентах. Поэтому:
\(1.8x^{2} > 1\cdot x^{2} > \frac{1}{3}x^{2}\) для любого \( x\neq 0. \)
При \(x = 0\) все функции равны нулю, но в задаче рассматриваются другие значения.
Вернуться к содержанию учебника