Упражнение 122 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 48
Вернуться к содержанию учебника
Вопрос
Покажите схематически, как расположен в координатной плоскости график функции:
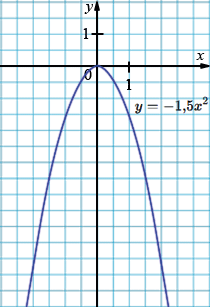
а) \(y = -1{,}5x^{2}\);
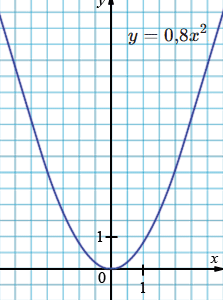
б) \(y = 0{,}8x^{2}\).
Перечислите свойства этой функции.
Подсказка
Вспомните:
- Что такое функция.
- Свойства функции.
- График функции.
- Квадратичную функцию и ее график.
- Положение точек на координатной плоскости.
- Числовые промежутки.
Ответ
а) \(y = -1{,}5x^{2}\)
Свойства:
1. \(D =(-\infty; +\infty) \)
2. \(E =(-\infty; 0] \)
3. \(y=0\) при \(x=0\)
4. \(y<0\) при \(x\ne0\)
5. Функция возрастает на \((-\infty; 0]\) и убывает на \([0; +\infty) \)
6. Наибольшее значение функции равно нулю при \(x=0. \)
3. Функция чётная, так как:
\( (-x)^2 = x^2. \)
б) \(y = 0{,}8x^{2}\).
Свойства:
1. \(D =(-\infty; +\infty) \)
2. \(E =[0; +\infty)\)
3. \(y=0\) при \(x=0\)
4. \(y>0\) при \(x\ne0\)
5. Функция возрастает на \([0; +\infty)\) и убывает на \((-\infty; 0]\)
6. Наименьшее значение функции равно нулю при \(x=0.\)
3. Функция чётная, так как:
\( (-x)^2 = x^2. \)
Пояснения:
Квадратичная функция имеет общий вид \(y = ax^{2}\). Если \(a>0\), то ветви параболы направлены вверх; если \(a<0\), ветви параболы направлены вниз. Вершина всегда в точке \(x=0\), если нет других слагаемых. Чётность гарантирует симметрию относительно оси \(y\).
а) Это парабола, ветви направлены вниз, так как коэффициент \(-1,5 < 0\). Парабола более «крутая», чем стандартная \(y = -x^{2}\), так как модуль коэффициента больше 1.
б) Это парабола, ветви направлены вверх, так как коэффициент \(0,8 > 0\). Парабола более «широкая», чем стандартная \(y=x^{2}\), так как \(0,8 < 1\).
Знак \(a\) определяет область значений:
\( a>0 \Rightarrow y\ge0, \quad a<0 \Rightarrow y\le0. \)
Вернуться к содержанию учебника