Упражнение 127 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 49

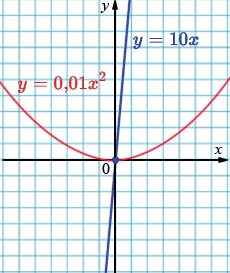
\( \begin{cases} y=0,01x^2 \\ y=10x \end{cases}\) 

\[ 0{,}01x^{2} = 10x\]

\[ 0{,}01x^{2} - 10x = 0. \]

\[ x(0{,}01x - 10) = 0 \]

\( x = 0 \)   или   \( 0{,}01x - 10 = 0 \)

                       \(0{,}01x = 10\)

                       \(x = 10:0{,}01\)

                       \( x = 1000\)

При \(x = 1000\):

\( y = 10x = 10\cdot1000 = 10000\)

Итак, имеем две общие точки:

1) \(O(0;\,0)\) — очевидная;
2) \(A(1000;\, 10000)\).

Ответ: графики имеют ещё одну общую точку: \((1000;\, 10000)\).

Пояснения:

— График \(y = 0,01x^{2}\) — парабола, ветви направлены вверх, «очень широкая», так как коэффициент 0.01 маленький.

— График \(y = 10x\) — прямая, проходящая через начало координат, достаточно крутая.

Когда мы решаем уравнение \[ 0{,}01x^{2} = 10x, \] мы ищем все \(x\), при которых значения функций равны, а значит точки с одинаковыми координатами лежат одновременно на двух графиках.

Первое решение — \(x = 0\) — даёт точку пересечения в начале координат. Второе решение — \(x = 1000\) — подтверждает, что парабола и прямая пересекаются ещё один раз в дальней части координатной плоскости.