Подобие произвольных фигур / Подобие фигур / Справочник по геометрии 7-9 класс

Определение

Фигура F₁называется подобной фигуре F, если она равна некоторой фигуре F*, гомотетичной фигуре F (риc. 1).

Рис. 1

Если

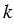— коэффициент гомотетии фигур F* и F, то положительное число

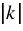называется коэффициентом подобия фигуры F₁ относительно фигуры F (или, коротко, коэффициентом подобия фигур F₁ и F).

Если фигура F₁ подобна фигуре F, то пишут: F₁

F с коэффициентом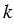

или F₁

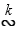F, где

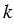— коэффициент подобия.

Подобие фигур обладает следующими свойствами:

а) если F₁

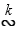F, то F

F₁;

б) если F₂

F₁ и F₁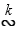

F, то F₂

F (рис. 2).

Рис. 2

Из определения подобия фигур следует, что если фигура F₁ гомотетична фигуре F с коэффициентом

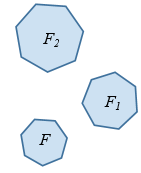
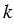, то F₁

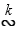F с коэффициентом

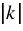. Таким образом, гомотетичные фигуры представляют собой частный случай подобных фигур.

Пользуясь свойствами гомотетии, а также свойствами равенства фигур, можно доказать, что фигурой, подобной прямой (отрезку, лучу, полуплоскости), является прямая (отрезок, луч, полуплоскость). Фигурой, подобной углу, является угол, равный данному. Из свойства 3⁰ гомотетии, также следует, что фигурой, подобной окружности, является окружность.