Задание 458 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№458 учебника 2013-2022 (стр. 122):
Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 220 м и 160 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
№458 учебника 2023-2024 (стр. 120):
Подсказка
№458 учебника 2013-2022 (стр. 122):
Вспомните:
- Какой четырехугольник называется квадратом.
- Как найти площадь квадрата.
- Какой четырехугольник называется прямоугольником.
- Как найти площадь прямоугольника.
- Что такое периметр многоугольника.
№458 учебника 2023-2024 (стр. 120):
Вспомните:
- Какой угол называют неразвернутым.
- Что такое биссектриса угла.
- Как построить биссектрису угла.
- Свойство биссектрисы угла.
- Что называют касательной к окружности, ее свойство.
- Как построить перпендикулярные прямые.
- Окружность, вписанная в угол.
Ответ
№458 учебника 2013-2022 (стр. 122):

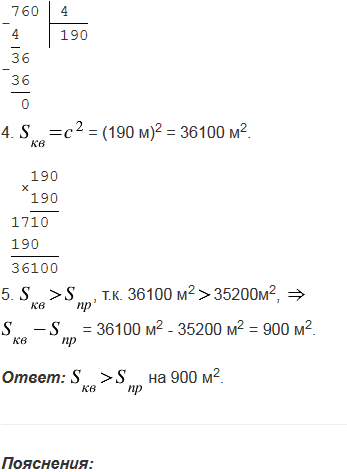



№458 учебника 2023-2024 (стр. 120):
Дано: 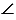 РНK - неразвернутый, А
РНK - неразвернутый, А 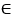 НР.
НР.
Построить: окружность, вписанную в 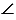 РНK и А ее точка касания.
РНK и А ее точка касания.
Решение:
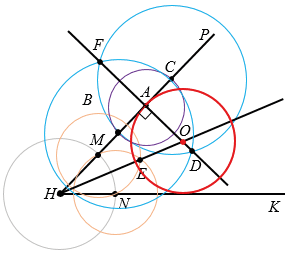
Окружность с центром О радиуса ОА - искомая окружность.
Пояснения:
Чертим 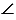 РНK и точку А, лежащую на стороне угла НР.
РНK и точку А, лежащую на стороне угла НР.
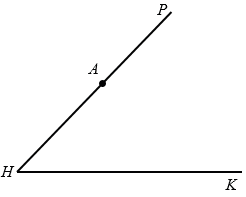
Строим биссектрису угла РНK:
1) строим окружность с центром в вершине угла РНK произвольного радиуса (полностью окружность строить необязательно), эта окружность пересечет стороны угла в точках М и N;
2) строим две окружности с центрами в точках М и N радиуса МN (полностью окружности строить необязательно, главное определить точку их пересечения внутри угла РНK), эти окружности пересекутся в точке Е.
3) проводим луч НЕ - биссектрису угла РНK.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Построим перпендикуляр к стороне НР угла РНК, проходящий через точку А:
1) строим окружность произвольного радиуса с центром в точке А, эта окружность пересечет НР в двух точках В и С;
2) строим две окружности с центрами в точках В и С радиуса ВС, эти окружности пересекутся в двух точках F и D;
3) чертим прямую FD, которая будет проходить через точку А перпендикулярно к НР и пересечет биссектрису НЕ в точке О.
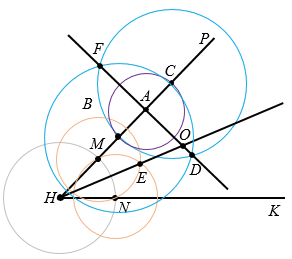
Далее чертим окружность с центром О радиуса ОА, которая и будет искомой окружностью, то есть эта окружность вписана в угол РНЕ и касается его стороны в данной точке А.
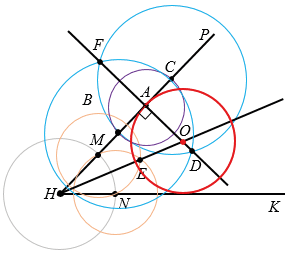
Вернуться к содержанию учебника