Задание 459 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№459 учебника 2013-2022 (стр. 126):
Пусть 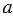 - основание, h - высота, а S - площадь параллелограмма. Найдите: а) S, если
- основание, h - высота, а S - площадь параллелограмма. Найдите: а) S, если 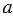 = 15 см, h = 12 см; б)
= 15 см, h = 12 см; б) 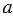 , если S = 34 см2, h = 8,5 см; в)
, если S = 34 см2, h = 8,5 см; в) 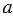 , если S = 162 см2, h =
, если S = 162 см2, h = 
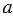 ; г) h, если h = 3
; г) h, если h = 3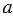 , S = 27.
, S = 27.
№459 учебника 2023-2024 (стр. 120):
Подсказка
№459 учебника 2013-2022 (стр. 126):
Вспомните:
- Что такое параллелограмм.
- Что такое площадь.
- Как найти площадь параллелограмма.
№459 учебника 2023-2024 (стр. 120):
Вспомните:
- Какой угол называют острым.
- Какие точки называют симметричными относительно прямой.
- Что называют треугольником, его периметр.
- Что такое отрезок, прямая.
- Какой треугольник называют равнобедренным.
- Медиана и высота треугольника.
- Как построить перпендикуляр к прямой.
- Серединный перпендикуляр к отрезку, его свойство.
Ответ
№459 учебника 2013-2022 (стр. 126):


№459 учебника 2023-2024 (стр. 120):
Дано:  МОК - острый, А - его внутренняя точка.
МОК - острый, А - его внутренняя точка.
Построить: точки В и С на сторонах  МОК такие, что РАВС будет наименьшим.
МОК такие, что РАВС будет наименьшим.
Решение:

Докажем, что РАВС - наименьший.
1. По построению точки А и А1 симметричны относительно ОМ,  ОМ - серединный перпендикуляр к отрезку АА1,
ОМ - серединный перпендикуляр к отрезку АА1,  АВ = А1В. Аналогично, АС = А1С.
АВ = А1В. Аналогично, АС = А1С.
2. РАВС = АВ + ВС + АС и
А1А2 = А1В + ВС + А2С, при этом
АВ = А1В и АС = А1С,  РАВС = А1А2,
РАВС = А1А2,  РАВС - наименьший. Что и требовалось доказать.
РАВС - наименьший. Что и требовалось доказать.
Пояснения:
Чертим острый угол МОК и точку А внутри его.

Теперь построим точки А1 и А2 симметричные точке А относительно сторон данного угла ОМ и ОК соответственно.
Сначала строим точку А1, симметричную точке А относительно ОМ:
1) чертим окружность с центром А произвольного радиуса так, чтобы она пересекла прямую ОМ в двух точках, обозначим их Е и Р;
2) чертим две окружности с центрами в точках Е и Р радиуса ЕА = РА, эти окружности пересекутся в двух точках одна из них точка А, а другая, симметричная ей относительно прямой ОМ, точка А1.
3) соединяем точки А и А1.
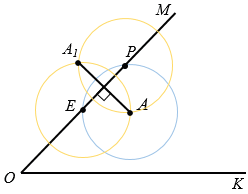
Аналогично строим точку А2, симметричную точке А относительно ОК.

Далее соединяем точки А1 и А2, отрезок А1А2 пересечет стороны угла в точках В и С. Соединяем точки А, В и С, получаем 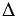 АВС.
АВС.

Докажем, что РАВС будет наименьшим.
По построению точки А и А1 симметричны относительно ОМ, значит, ОМ - серединный перпендикуляр к отрезку АА1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка, значит, АВ = А1В. Аналогично, АС = А1С.
Получается:
РАВС = АВ + ВС + АС и
А1А2 = А1В + ВС + А2С, при этом
АВ = А1В и АС = А1С, значит, РАВС = А1А2.
Кратчайшее расстояние между двумя точками - это длина отрезка соединяющего это точки. следовательно, РАВС - наименьший. Что и требовалось доказать.
Вернуться к содержанию учебника