Упражнение 118 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№118 учебника 2023-2025 (стр. 30):
Запишите без скобок выражение:
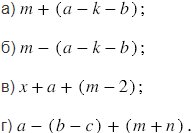
№118 учебника 2013-2022 (стр. 27):
Какое из уравнений не имеет корней?
1. \(2(x + 3) = 2x + 6\);
2. \(2y = 4y\);
3. \(4(c - 2) = 3c - 6\);
4. \(3x + 11 = 3(x + 4)\).
Подсказка
№118 учебника 2023-2025 (стр. 30):
Вспомните:
№118 учебника 2013-2022 (стр. 27):
Вспомните:
- Что называют корнем уравнения.
- Решение уравнений.
- Подобные слагаемые.
Ответ
№118 учебника 2023-2025 (стр. 30):
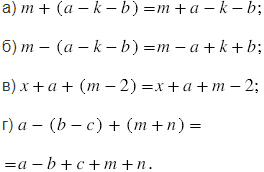
Пояснения:
Раскрытие скобок выполняется по следующим правилам:
- если перед скобками стоит знак "плюс", то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки;
- если перед скобками стоит знак "минус", то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки, на противоположный.
№118 учебника 2013-2022 (стр. 27):
1. \(2(x + 3) = 2x + 6;\)
\(2x + 6 = 2x + 6;\)
\(2x-2x = 6-6;\)
\(0x=0\) - имеет бесконечно много корней.
2. \(2y = 4y;\)
\(2y - 4y = 0;\)
\(-2y = 0;\)
\(y = 0\).
Есть один корень.
3. \(4(c - 2) = 3c - 6;\)
\(4c - 8 = 3c - 6;\)
\(4c - 3c = -6 + 8;\)
\(c = 2\).
Есть один корень.
4. \(3x + 11 = 3(x + 4);\)
\(3x + 11 = 3x + 12;\)
\(3x - 3x = 12 - 11;\)
\(0 = 1\) - корней нет.
Ответ: уравнение 4 не имеет корней.
Пояснения:
Уравнение тождественное – верно при любых значениях переменной (п. 1).
Уравнение разрешимое – имеет конечное число решений (п. 2 и 3).
Уравнение противоречивое – приводит к ложному равенству типа \(0= k\), где \(k\neq0\), и не имеет корней (п. 4).
Чтобы проверить уравнение, раскрываем скобки, собираем подобные и смотрим на полученное равенство: если получается тождество, корней бесконечно; если противоречие – корней нет; иначе находим конкретные значения переменной.
Вернуться к содержанию учебника