Упражнение 333 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№333 учебника 2023-2025 (стр. 79):
Какое из чисел \(0{,}6;\;\frac{142}{29};\;3;\;\sqrt{33}\) отмечено на координатной прямой точкой A (рис. 15)?
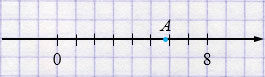
Рис. 15
№333 учебника 2013-2022 (стр. 80):
Найдите значение выражения \(\dfrac{|x|}{x}\) при \(x = -8;\ -5;\ 1;\ 7;\ 128.\)
Чему равно значение выражения \(\dfrac{|x|}{x}\), если:
а) \(x > 0;\) б) \(x < 0?\)
Подсказка
№333 учебника 2023-2025 (стр. 79):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Умножение десятичных дробей.
- Положение чисел на координатной прямой.
- Деление и дроби.
№333 учебника 2013-2022 (стр. 80):
Вспомните:
Ответ
№333 учебника 2023-2025 (стр. 79):
1) \(0{,}6\) - не соответствует точке А.
2) \( \frac{142}{29}=4{,}896\dots\) - не соответствует точке А.
| - | 1 | 4 | 2 | 2 | 9 | ||||||||||||
| 1 | 1 | 6 | 4 | , | 8 | 9 | 6 | . | . | . | |||||||
| - | 2 | 6 | 0 | ||||||||||||||
| 2 | 3 | 2 | |||||||||||||||
| - | 2 | 8 | 0 | ||||||||||||||
| 2 | 6 | 1 | |||||||||||||||
| - | 1 | 9 | 0 | ||||||||||||||
| 1 | 7 | 4 | |||||||||||||||
| 1 | 6 |
3) \(3\) - не соответствует точке А.
4) \(\sqrt{33}=5{,}7\dots\) - соответствует точке А.
\(\sqrt{25}<\sqrt{33}<\sqrt{36}\)
\(5<\sqrt{33}<6\)
\(5,1^2 = 26,01\)
\(5,2^2 = 27,04\)
\(5,3^2 = 28,09\)
\(5,4^2 = 29,16\)
\(5,5^2 = 30,25\)
\(5,6^2 = 31,36\)
\(5,7^2 = 32,49\)
\(5,8^2 = 33,64\)
\(5,7<\sqrt{33}<5,8\)
Ответ: \(А(\sqrt{33})\).
Пояснения:
Чтобы определить, какое из чисел отмечено на координатной прямой точкой А, учитываем то, что:
- в случае с числом \( \frac{142}{29}\) черту дроби можно заменить делением (числитель разделить на знаменатель);
- в случае с числом \(\sqrt{33}\) арифметический квадратный корень из числа \(a\) — это такое неотрицательное число \(x\), при котором \(x^2 = a\).
№333 учебника 2013-2022 (стр. 80):
\(\dfrac{|x|}{x}\)
Если \(x = -8\), то
\(\dfrac{|-8|}{-8} = \dfrac{8}{-8} = -1.\)
Если \(x = -5\), то
\(\dfrac{|-5|}{-5} = \dfrac{5}{-5} = -1.\)
Если \(x = 1\), то
\(\dfrac{|1|}{1} = \dfrac{1}{1} = 1.\)
Если \(x = 7\)
\(\dfrac{|7|}{7} = \dfrac{7}{7} = 1.\)
Если \(x = 128\), то
\(\dfrac{|128|}{128} = \dfrac{128}{128} = 1.\)
а) \(\frac{|x|}{x} = 1\), если \( x > 0\).
б) \(\frac{|x|}{x} = -1\), если \(x < 0\)
Пояснения:
Используем определение модуля:
\[ |x| = \begin{cases} x, & \text{если } x > 0;\\ -x, & \text{если } x < 0. \end{cases} \]
Выражение \(\dfrac{|x|}{x}\) показывает знак числа \(x\): оно равно \(1\) для положительных чисел и \(-1\) для отрицательных. При \(x = 0\) выражение не имеет смысла, так как знаменатель равен нулю.
Вернуться к содержанию учебника