Упражнение 549 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№549 учебника 2023-2025 (стр. 127):
Решите уравнения:
а) \(0{,}7x^2 = 1{,}3x + 2\);
б) \(7 = 0{,}4y + \frac{1}{5}y^2\);
в) \(x^2 - 1{,}6x - 0{,}36 = 0\);
г) \(z^2 - 2z + 2{,}91 = 0\);
д) \(0{,}2y^2 - 10y + 125 = 0\);
е) \(\frac{1}{3}x^2 + 2x - 9 = 0\).
№549 учебника 2013-2022 (стр. 129):
(Для работы в парах.) Решить графически уравнение:
а) \(x^2 - 2x - 1 = 0;\)
б) \(x^2 - 4x + 2 = 0.\)
1) Обсудите друг с другом, в каком виде удобно представить уравнение.
2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их.
3) Найдите корни каждого из уравнений с помощью формулы корней квадратного уравнения и сравните их со значениями, найденными при графическом решении.
Подсказка
№549 учебника 2023-2025 (стр. 127):
Вспомните:
- Решение полных квадратных уравнений (дискриминант).
- Свойства уравнений.
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Противоположные числа.
- Деление и дроби.
- Сокращение дробей.
- Неправильные дроби.
- Смешанные числа.
- Умножение десятичных дробей.
- Умножение обыкновенных дробей.
- Деление десятичных дробей.
№549 учебника 2013-2022 (стр. 129):
Вспомните:
- Линейную функцию, ее график.
- Квадратичную функцию, ее график.
- Координаты точки.
- Решение полных квадратных уравнений (дискриминант).
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Свойства уравнений.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Противоположные числа.
- Деление и дроби.
- Десятичная запись дробных чисел.
Ответ
№549 учебника 2023-2025 (стр. 127):
а) \( 0{,}7x^2 - 1{,}3x - 2 = 0 \) \(/\times10\)
\(7x^2 - 13x - 20 = 0\)
\(a=7\), \(b=-13\), \(c=-20\).
\(D = b^2 - 4ac =\)
\(=(-13)^2 - 4\cdot7\cdot(-20) =\)
\(=169 + 560 = 729\); \(\sqrt D = 27\)
\(x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-13) + 27}{2\cdot7} =\)
\(=\frac{40}{14} = \frac{20}{7} = 2\frac{6}{7}\)
\(x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-(-13) - 27}{2\cdot7} =\)
\(= \frac{-14}{14} = -1 \).
Ответ: \(x_1 = 2\frac{6}{7}\), \(x_2 =-1\).
б) \( 7 = 0{,}4y + \frac{1}{5}y^2 \)
\(\frac{1}{5}y^2 + 0{,}4y - 7 = 0 \) \(/\times5\)
\(y^2 + 2y - 35 = 0\)
\(a=1\), \(b=2\), \(c=-35\).
\(D =b^2 - 4ac = 2^2 - 4\cdot1\cdot(-35) =\)
\(=4 + 140 = 144\), \(\sqrt D = 12\).
\(y_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-2 + 12}{2} =\)
\(=\frac{10}{2} =5\).
\(y_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-2 - 12}{2} =\)
\(=\frac{-14}{2} =-7\).
Ответ: \(y_1 = 5\), \(y_2 =-7\).
в) \( x^2 - 1{,}6x - 0{,}36 = 0\)
\(a=1\), \(b=-1,6\), \(c=-0,36\).
\(D = b^2 - 4ac =\)
\(=(-1{,}6)^2 - 4\cdot1\cdot(-0{,}36) =\)
\(=2{,}56 + 1{,}44 = 4\); \(\sqrt D = 2\)
\(x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-1{,}6) + 2}{2} =\)
\(=\frac{3{,}6}{2} = 1{,}8\).
\(x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-(-1{,}6) - 2}{2} =\)
\( = \frac{-0{,}4}{2} = -0{,}2 \).
Ответ: \(x_1 =1,8\), \(x_2 = -0,2\).
г) \( z^2 - 2z + 2{,}91 = 0\)
\(a=1\), \(b=-2\), \(c=-0,36\).
\( D = b^2 - 4ac =\)
\(=(-2)^2 - 4\cdot1\cdot2{,}91 =\)
\(=4 - 11{,}64 = -7{,}64 < 0\)
Ответ: корней нет.
д) \( 0{,}2y^2 - 10y + 125 = 0 \) \(/\times5\)
\(y^2 - 50y + 625 = 0\)
\(a=1\), \(b=-50\), \(c=625\).
\(D = b^2 - 4ac =\)
\(=(-50)^2 - 4\cdot1\cdot625 =\)
\(=2500 - 2500 = 0\)
\( y =-\frac{b}{2a}= -\frac{-50}{2} = 25\)
Ответ: \(y=25\).
е) \( \frac{1}{3}x^2 + 2x - 9 = 0 \) \(/\times3\)
\(x^2 + 6x - 27 = 0\)
\(a=1\), \(b=6\), \(c=-27\).
\(D = b^2 - 4ac = 6^2 - 4\cdot1\cdot(-27) =\)
\(=36 + 108 = 144\); \(\sqrt D = 12\)
\(x_1 = \frac{-b + \sqrt{D}}{2a} =\frac{-6 + 12}{2}=\)
\(=\frac{6}{2}= 3\).
\(x_2 = \frac{-b - \sqrt{D}}{2a} =\frac{-6 - 12}{2}=\)
\(=\frac{-18}{2}= -9\).
Ответ: \(x_1 = 3\), \(x_2 = -9\).
Пояснения:
Приводим каждое равенство к стандартному квадратному виду \(ax^2+bx+c=0\). Для этого сначала переносим все слагаемые из правой части уравнения в левую, изменив их знаки на противоположные. Для удобства вычислений там, где это необходимо, умножаем обе части уравнение на такое число, чтобы коэффициенты \(a\), \(b\) и \(c\) стали целочисленными. Решаем полученное квадратное уравнение.
Количество корней полного квадратного уравнения зависит от дискриминанта. Формула дискриминанта:
\(D=b^2-4ac\).
– если \(D>0\), то уравнение имеет два корня:
\(x_1 =\frac{-b+\sqrt{D}}{2a}\);
\(x_2 =\frac{-b-\sqrt{D}}{2a}\).
– если \(D=0\), то уравнение имеет один корень:
\(x =-\frac{b}{2a}\).
– если \(D<0\), то уравнение не имеет корней.
№549 учебника 2013-2022 (стр. 129):
а) \(x^2 - 2x - 1=0\)
\(x^2 = 2x + 1\)
\(y = x^2\) - парабола.
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
\(y = 2x + 1\) - прямая.
| \(x\) | 0 | 2 |
| \(y\) | 1 | 5 |
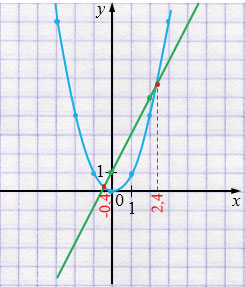
\(x^2 - 2x - 1=0\)
\(a = 1\), \(b = -2\), \(c = -1\)
\(D =b^2 - 4ac =\)
\(=(-2)^2 -4\cdot1\cdot(-1) =\)
\(=4+4 = 8\);
\(\sqrt{D} = \sqrt{8} =\sqrt{4\cdot2}=2\sqrt{2}\)
\( x_1 = \frac{-b+\sqrt{D}}{2a}= \frac{-(-2)+ 2\sqrt{2}}{2\cdot1}=\)
\(=\frac{2+ 2\sqrt{2}}{2}=\frac{\cancel2(1+ \sqrt{2})}{\cancel2}=\)
\(=1+ \sqrt{2}\approx1+1,4 \approx2,4\).
\( x_2 = \frac{-b-\sqrt{D}}{2a}= \frac{-(-2)- 2\sqrt{2}}{2\cdot1}=\)
\(=\frac{2- 2\sqrt{2}}{2}=\frac{\cancel2(1- \sqrt{2})}{\cancel2}=\)
\(=1- \sqrt{2}\approx1-1,4 \approx-0,4\).
Ответ: \( x_1 \approx2,4\), \( x_2 \approx-0,4\).
б) \( x^2 - 4x + 2=0\)
\( x^2 = 4x - 2\)
\(y = x^2\) - парабола.
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
\(y= 4x - 2\)
| \(x\) | 0 | 1 |
| \(y\) | -2 | 2 |

\( x^2 - 4x + 2=0\)
\(a = 1\), \(b = -4\), \(c = 2\)
\(D =b^2 - 4ac = (-4)^2 -4\cdot1\cdot2 = \)
\(=16-8 = 8\);
\(\sqrt{D} = \sqrt{8} =\sqrt{4\cdot2}=2\sqrt{2}\)
\( x_1 = \frac{-b+\sqrt{D}}{2a}= \frac{4 + 2\sqrt{2}}{2} =\)
\(=\frac{\cancel2(2 + \sqrt{2})}{\cancel2} =2 + \sqrt2\approx\)
\(\approx 2+1,4 \approx 3,4 \).
\( x_2 = \frac{-b-\sqrt{D}}{2a}= \frac{4 - 2\sqrt{2}}{2} =\)
\(=\frac{\cancel2(2 - \sqrt{2})}{\cancel2} =2 - \sqrt2 \approx\)
\(\approx2-1,4 \approx 0,6 \).
Ответ: \( x_1 \approx3,4\), \( x_2 \approx0,6\).
Пояснения:
1 способ
Чтобы решить уравнения графически, в левой части уравнения оставляем \(x^2\), а остальные компоненты переносим в правую часть,изменив их знаки на противоположные. Строим два графика:
- \(y = x^2\) - парабола. Строим по точкам;
- \(y = kx+b\) - прямая. Для построения достаточно двух точек.
Абсциссы (координаты \(x\)) точек пересечения графиков и будут решениями исходного уравнения.
2 способ
Количество корней полного квадратного уравнения
\(ax^2+bx+c=0\) зависит от дискриминанта. Формула дискриминанта:
\(D=b^2-4ac\).
– если \(D>0\), то уравнение имеет два корня:
\(x_1 =\frac{-b+\sqrt{D}}{2a}\);
\(x_2 =\frac{-b-\sqrt{D}}{2a}\).
– если \(D=0\), то уравнение имеет один корень:
\(x =-\frac{b}{2a}\).
– если \(D<0\), то уравнение не имеет корней.
Вернуться к содержанию учебника