Упражнение 1067 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1067 учебника 2023-2025 (стр. 237):
Известно, что \(f(x)=-5x+6\). Найдите значение \(x\), при котором:
а) \(f(x)=17\);
б) \(f(x)=-3\);
в) \(f(x)=0\).
№1067 учебника 2013-2022 (стр. 245):
Постройте в одной системе координат графики функций \(y=x^{-1}\), где \(x>0\), и \(y=x^{-2}\), где \(x>0\). Сравните значения \(x^{-1}\) и \(x^{-2}\), если:
а) \(0 < x < 1\);
б) \(x > 1\).
Подсказка
№1067 учебника 2023-2025 (стр. 237):
Вспомните:
- Что такое функция.
- Значение функции.
- Свойства уравнений.
- Деление и дроби.
- Сложение и вычитание рациональных чисел.
- Деление десятичных дробей.
№1067 учебника 2013-2022 (стр. 245):
Вспомните:
- Графики функций \(y=x^{-1}\) и \(y=x^{-2}\).
- Степень с целым отрицательным показателем.
- Деление и дроби.
- Деление десятичных дробей.
- Координаты точки на координатной плоскости.
Ответ
№1067 учебника 2023-2025 (стр. 237):
\(f(x)=-5x+6\).
а)\(f(x)=17\):
\(-5x+6=17\)
\(-5x=17-6\)
\(-5x=11\)
\(x=-\frac{11}{5}\)
\(x=-2,2.\)
Ответ: \(x=-2,2.\)
б) \(f(x)=-3\):
\(-5x+6=-3 \)
\(-5x=-3-6\)
\(-5x=-9\)
\(x=\frac{9}{5}\)
\(x=1,8.\)
Ответ: \(x=1,8.\)
в) \(f(x)=0\):
\(-5x+6=0\)
\(-5x=-6\)
\(x=\tfrac{6}{5}\)
\(x=1,2.\)
Ответ: \(x=1,2.\)
Пояснения:
1) Функция задана формулой \(f(x)=-5x+6\). Чтобы найти значение \(x\), при котором функция принимает данное значение, нужно составить уравнение \(-5x+6=y\), где \(y\) — известное число.
2) В каждом пункте решаем линейное уравнение: переносим известные числа вправо, получаем \(-5x=\dots\), а затем делим обе части на \(-5\).
3) В итоге:
а) \(x=-2,2\);
б) \(x=1,8\);
в) \(x=1,2\).
№1067 учебника 2013-2022 (стр. 245):
\(y = x^{-1} = \frac1x\), где \(x>0\)
| \(x\) | 0,5 | 1 | 2 |
| \(y\) | 2 | 1 | 0,5 |
\(y=x^{-2}=\frac{1}{x^2}\), где \(x>0\).
| \(x\) | 0,5 | 1 | 2 |
| \(y\) | 4 | 1 | 0,25 |
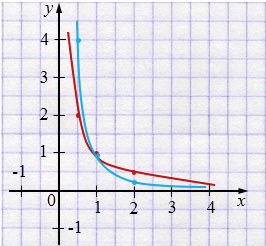
а) При \(0 < x < 1\):
\(x^{-2} > x^{-1}\)
б) При \(x > 1\):
\(x^{-2} < x^{-1}\)
Пояснения:
Функции \(y = x^{-1}\) и \(y=x^{-2}\) при \(x>0\) расположены в 1 координатной четверти и пересекаются в точке с координатами \((1; 1)\).
При \(0 < x < 1\) график функции
\(y=x^{-2}\) расположен выше графика функции \(y = x^{-1} \), значит, \(x^{-2} > x^{-1}\) при \(0 < x < 1\).
При \(x > 1\) график функции \(y=x^{-2}\) расположен ниже графика функции \(y = x^{-1} \), значит, \(x^{-2} < x^{-1}\) при \(x > 1\).
Вернуться к содержанию учебника