Упражнение 1120 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(f(x) = -1{,}5x + 6\)

\(0 \le f(x) \le 3\)

\(0 \le -1{,}5x + 6 \le 3\)

\(0 - 6 \le -1{,}5x + 6 - 6 \le 3 - 6\)

\(-6 \le -1{,}5x \le -3\)   \(/ : (-1,5)\)

\(\frac{6}{1,5} \ge x \ge \frac{3}{1,5}\)

\(\frac{60}{15} \ge x \ge \frac{30}{15}\)

\(4 \ge x \ge 2\)

\( 2 \le x \le 4\)

\(y = -1{,}5x + 6\)

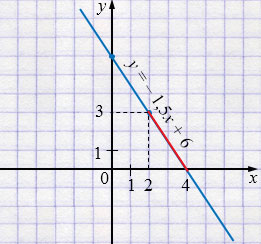
Ответ: \(0 \le f(x) \le 3\) при \(x \in [2;\,4].\)

Пояснения:

Алгебраический способ:

Чтобы ответить на вопрос задачи алгебраически, нужно решить двойное неравенство:

\(0 \le -1{,}5x + 6 \le 3\).

При решении неравенства использовали следующие свойства:

- если к частям верного неравенства прибавить одно и то же число, то получится верное неравенство;

- если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.

Получаем, что значения функции

\(0 \le f(x) \le 3\) при \(x \in [2; 4]\)

Графическая иллюстрация:

Функция \(f(x) = -1{,}5x + 6\) — линейная, угловой коэффициент отрицателен (\(k = -1{,}5 < 0\)), значит, функция убывает. Графиком линейной функции является прямая. График строят по двум точкам, так как прямая однозначно задается двумя точками.

На графике участок, где \(0 \le f(x) \le 3\), соответствует \(x \in [2; 4]\).

\(x^{2} - y^{2} = 69\)

\(x\) и \(y\) - натуральные числа.

\( (x - y)(x + y) = 69\)

\( 69 = 1 \cdot 69 = 3 \cdot 23 = 23\cdot3 = 69 \cdot1\)

1) \(\begin{cases}x - y = 1, \\ x + y = 69\end{cases}\)    \((+)\)

\(\begin{cases} 2x = 70,   / : 2 \\ x + y = 69\end{cases}\)

\(\begin{cases} x = \frac{70}{2}, \\ y = 69 - x \end{cases}\)

\(\begin{cases} x = 35, \\ y = 69 - 35 \end{cases}\)

\(\begin{cases} x = 35, \\ y =34 \end{cases}\)

2) \(\begin{cases}x - y = 3, \\ x + y = 23 \end{cases}\)    \((+)\)

\(\begin{cases} 2x = 26,  / : 2 \\ x + y = 23 \end{cases}\)

\(\begin{cases} x = \frac{26}{2}, \\ y = 23 - x \end{cases}\)

\(\begin{cases} x = 13, \\ y = 23 - 13 \end{cases}\)

\(\begin{cases} x = 13, \\ y = 10 \end{cases}\)

3) \(\begin{cases}x - y = 69, \\ x + y = 1\end{cases}\)    \((+)\)

\(\begin{cases} 2x = 70,   / : 2 \\ x + y = 1\end{cases}\)

\(\begin{cases} x = \frac{70}{2}, \\ y = 1 - x \end{cases}\)

\(\begin{cases} x = 35, \\ y = 1 - 35 \end{cases}\)

\(\begin{cases} x = 35, \\ y =-34 \end{cases}\)

\(-34\) - не является натуральным.

4) \(\begin{cases}x - y = 23, \\ x + y = 3 \end{cases}\)    \((+)\)

\(\begin{cases} 2x = 26,  / : 2 \\ x + y = 3 \end{cases}\)

\(\begin{cases} x = \frac{26}{2}, \\ y = 3 - x \end{cases}\)

\(\begin{cases} x = 13, \\ y = 3 - 13 \end{cases}\)

\(\begin{cases} x = 13, \\ y = -10 \end{cases}\)

\(-10\) - не является натуральным числом.

Пояснения:

Формула разности квадратов: \[ x^{2} - y^{2} = (x - y)(x + y). \] Позволяет заменить квадратное уравнение на линейное с целыми множителями.

Учитывая то, что \(x\) и \(y\) по условию натуральные числа, разность \(x - y\) и сумма \(x + y\) также будут натуральными числами, тогда:

\( 69 = 1 \cdot 69 = 3 \cdot 23 = 23\cdot3 = 69 \cdot1\).

Далее, учитывая полученные множители, составляем системы уравнений с двумя переменными и решаем их способом сложения.