Упражнение 1143 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\( y = \{x\} \)

\[ \{x\} = x - [x], \] где \([x]\) — целая часть числа \(x\).

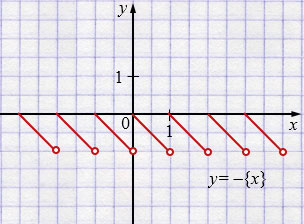
Пояснения:

Целой частью числа \(x\) называется наибольшее целое число, не превосходящее \(x\). Целая часть числа \(a\) обозначается так: \([x]\).

Дробная часть числа — это разность между числом и его целой частью, дробная часть числа \(x\) обозначается так: \(\{x\}\) и \(\{x\} = x - [x]\). Дробная часть числа всегда неотрицательна: \(0 \le \{a\} < 1.\)

Функция \( y = -\{x\} \) получается отражением графика \( y = \{x\} \) относительно оси \(OX\).

Следовательно, на каждом промежутке \( [n; n+1) \):

\( y = -\{x\} = -x + n, \) \(n\) - целое число,

и значения функции изменяются от 0 (при \(x = n\)) до \(-1\).

График функции \( y = \{x\} \) состоит из отрезков, направленных вниз, начиная с точки \((n; 0)\) и заканчивающихся в точке \((n+1; -1)\), где правая точка каждого отрезка не входит в график (открытая точка).

• Функция \( y = -\{x\} \) принимает значения в диапазоне \( [-1; 0] \).
• График повторяется через каждый интервал длины 1.
• При переходе через целое значение \(x\) происходит скачок от \(-1\) до \(0\).

\(y = -\dfrac{1}{\sqrt{x}}\).

Область определения: \( x > 0. \)

Пояснения:

Функция \(y = \dfrac{1}{\sqrt{x}}\) — это положительная ветвь, спадающая на промежутке \(x > 0\). При добавлении минуса перед выражением \(y = -\dfrac{1}{\sqrt{x}}\) график отражается относительно оси \(x\), то есть располагается ниже оси \(x\). Строим график по точкам, подбирая такие значения \(x\), удовлетворяющие ОДЗ, из которых извлекается квадратный корень.

Если \(x=\frac14\), то

\(y = -\dfrac{1}{\sqrt{\frac14}}=-\dfrac{1}{\frac12} =-2.\)

Если \(x=1\), то

\(y = -\dfrac{1}{\sqrt{1}}= -\dfrac{1}{1}=-1.\)

Если \(x=4\), то

\(y = -\dfrac{1}{\sqrt{4}}= -\dfrac{1}{2}.\)

Если \(x=9\), то

\(y = -\dfrac{1}{\sqrt{9}}= -\dfrac{1}{3}.\)