Упражнение 1147 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 257
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1147 учебника 2023-2025 (стр. 257):
Функция задана формулой \( y = \dfrac{1}{x^2 + 1} \). Пересекает ли её график ось \(x\)? ось \(y\)? В каких координатных четвертях расположен график этой функции?
№1147 учебника 2013-2022 (стр. 257):
Постройте график функции:
а) \(\displaystyle y=\frac{2x+3}{x}\);
б) \(\displaystyle y=\frac{4-5x}{x}\);
в) \(\displaystyle y=\frac{12}{x-4}\);
г) \(\displaystyle y=-\,\frac{6}{x+3}\).
Подсказка
№1147 учебника 2023-2025 (стр. 257):
Вспомните:
- Что называют функцией, ее график.
- Координаты точки.
- Степень с натуральным показателем.
№1147 учебника 2013-2022 (стр. 257):
Вспомните:
- Что называют функцией, ее график.
- Функция обратной пропорциональности.
- Координаты точки на координатной плоскости.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
- Десятичная запись дробных чисел.
- Сложение и вычитание десятичных дробей.
Ответ
№1147 учебника 2023-2025 (стр. 257):
1) С осью \(y\): \(x = 0\).
\( y = \frac{1}{0^2 + 1} = 1. \)
\((0; 1)\) - точка пересечения с осью \(y\).
С осью \(x\): \(y = 0\).
\( \frac{1}{x^2 + 1} = 0\) - нет корней, так как \(\dfrac{1}{x^2 + 1} > 0\) для любого \(x\), поэтому график ось \(x\) не пересекает.
2) Знаменатель \(x^2 + 1 > 0\) при любом \(x\), значит, \(y = \dfrac{1}{x^2 + 1} > 0\) при любом \(x\). Тогда график функции расположен выше оси \(x\), то есть в I и II координатных четвертях.
Ответ: график пересекает ось \(y\) в точке \((0; 1)\), не пересекает ось \(x\) и расположен в I и II координатных четвертях.
Пояснения:
Функция \(y = \dfrac{1}{x^2 + 1}\):
- определена для любого значения \(x\);
- всегда положительна, так как знаменатель \(x^2 + 1 > 0\) и поэтому не пересекает ось \(x\);
- ось \(y\) функция пересекает при \(x = 0\) в точке \((0; 1)\).
Поэтому график функции \(y = \dfrac{1}{x^2 + 1}\) полностью расположенная выше оси \(x\), то есть в I и II координатных четвертях.
№1147 учебника 2013-2022 (стр. 257):
а) \(\displaystyle y=\frac{2x+3}{x}=2+\frac{3}{x}\),
Область определения: \(x\ne0\).
| \(x\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) | \(-0,5\) |
| \(y\) | \(1,5\) | \(1\) | \(0,5\) | \(-1\) | \(-4\) |
| \(x\) | \(0,5\) | \(1\) | \(2\) | \(3\) | \(6\) |
| \(y\) | \(8\) | \(5\) | \(3,5\) | \(3\) | \(2,5\) |

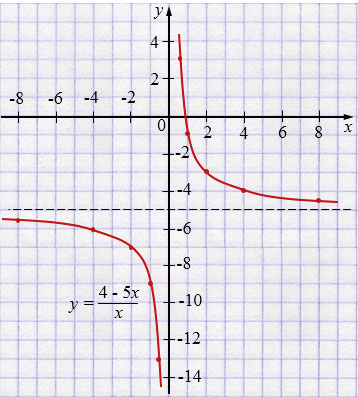
б) \(\displaystyle y=\frac{4-5x}{x}=\frac{4}{x}-5\),
Область определения: \(x\ne0\).
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(-0,5\) |
| \(y\) | \(-5,5\) | \(-6\) | \(-7\) | \(-9\) | \(-13\) |
| \(x\) | \(0,5\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y\) | \(3\) | \(-1\) | \(-3\) | \(-4\) | \(-4,5\) |
в) \(\displaystyle y=\frac{12}{x-4}\),
Область определения: \(x\ne4\).
| \(x\) | \(-8\) | \(-2\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(-1\) | \(-2\) | \(-3\) | \(-4\) | \(-6\) | \(-12\) |
| \(x\) | \(5\) | \(6\) | \(5\) | \(8\) | \(10\) | \(16\) |
| \(y\) | \(12\) | \(6\) | \(4\) | \(3\) | \(2\) | \(1\) |

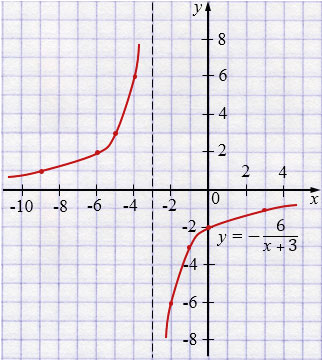
г) \(\displaystyle y=-\,\frac{6}{x+3}\),
Область определения: \(x\ne-3\).
| \(x\) | \(-9\) | \(-6\) | \(-5\) | \(-4\) |
| \(y\) | \(1\) | \(2\) | \(3\) | \(6\) |
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(3\) |
| \(y\) | \(-6\) | \(-3\) | \(-2\) | \(1\) |
Пояснения:
Использованные правила.
Деление многочлена на \(x\) раскладываем как \(\displaystyle \frac{ax+b}{x}=a+\frac{b}{x}\).
График \(\displaystyle y=\frac{k}{x}\) — гипербола с асимптотами \(x=0\) и \(y=0\). Сдвиги: \(\displaystyle y=a+\frac{k}{x}\) — вертикальный сдвиг на \(a\) (горизонтальная асимптота \(y=a\)); \(\displaystyle y=\frac{k}{x-h}\) — горизонтальный сдвиг на \(h\) (вертикальная асимптота \(x=h\)).
а) \(\displaystyle y=2+\frac{3}{x}\).
Это гипербола \(\displaystyle \frac{3}{x}\), сдвинутая вверх на \(2\). Поэтому вертикальная асимптота остаётся \(x=0\), горизонтальная становится \(y=2\). Знаки: при \(x>0\) \(y>2\); при \(x<0\) \(y<2\).
б) \(\displaystyle y=-5+\frac{4}{x}\).
Сдвиг гиперболы \(\displaystyle \frac{4}{x}\) вниз на \(5\). Асимптоты: \(x=0\), \(y=-5\).
в) \(\displaystyle y=\frac{12}{x-4}\).
Это гипербола, сдвинутая вправо на \(4\). Асимптоты: \(x=4\), \(y=0\). Значения \(y\) положительны при \(x>4\) и отрицательны при \(x<4\). Пересечения с осью \(Ox\) нет, так как дробь с ненулевым числителем не равна нулю.
г) \(\displaystyle y=-\frac{6}{x+3}\).
Гипербола, сдвинутая влево на \(3\) и отражённая по знаку. Асимптоты: \(x=-3\), \(y=0\). Ветвь во II четверти (при \(x<-3\)) выше оси \(Ox\), во IV четверти (при \(x>-3\)) ниже оси \(Ox\).
Асимптота — это прямая, к которой график функции неограниченно приближается, но никогда не пересекает.
Вернуться к содержанию учебника