Упражнение 1310 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 285
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1310 учебника 2023-2025 (стр. 285):
Постройте график функции, заданной формулой:
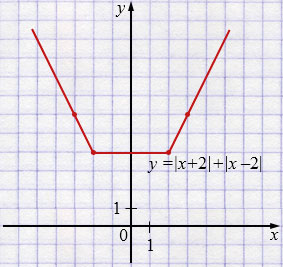
а) \(y=|x+2|+|x-2|\);
б) \(y=|x+1|-|x-1|\).
Подсказка
№1310 учебника 2023-2025 (стр. 285):
Вспомните:
- Что называют функцией, ее график.
- Модуль числа.
- Раскрытие скобок, подобные слагаемые.
- Числовые промежутки.
- Координаты точки на координатной плоскости.
Ответ
№1310 учебника 2023-2025 (стр. 285):
а) \(y=|x+2|+|x-2|\)
\(x + 2 = 0, \Rightarrow x = -2\)
\(x - 2 = 0, \Rightarrow x = 2\)
Знаки модулей на числовой прямой:
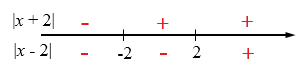
Если \(x < -2\), то
\(y = -\,(x+2)-(x-2)=\)
\(=-x - \cancel2-x + \cancel2=-2x\).
Если \(-2 \le x \le 2\), то
\(y=(x+2)-\bigl(x-2\bigr)\)
\(=\cancel x + 2 - \cancel x + 2 =4\).
Если \(x > 2\), то
\(y=(x+2)+(x-2)=\)
\(=x + \cancel 2 + x - \cancel 2 =2x\).
\( y= \begin{cases} -2x, \, если\, x < -2,\\ 4, -2\le x\le 2,\\ 2x,\,если\, x > 2 \end{cases} \)
\(y=-2x\), если \(x < 2\)
| \(x\) | \(-3\) | \(-2\) |
| \(y\) | \(6\) | \(4\) |
\(y=2x\), если \(x > 2\)
| \(x\) | \(3\) | \(2\) |
| \(y\) | \(6\) | \(4\) |
б) \(y=|x+1|-|x-1|\)
\(x + 1 = 0, \Rightarrow x = -1\)
\(x - 1 = 0, \Rightarrow x = 1\)
Знаки модулей на числовой прямой:

Если \(x < -1\), то
\(y = -\,(x+1)+(x-1)=\)
\(=-\cancel x - 1+\cancel x - 1=-2\).
Если \(-1 \le x \le 1\), то
\(y=(x+1)+\bigl(x-1\bigr)\)
\(=x +\cancel1 + x - \cancel1 =2x\).
Если \(x > 1\), то
\(y=(x+1)-(x-1)=\)
\(=\cancel x + 1 - \cancel x + 1 =2\).
\[ y= \begin{cases} -2, \, если\, x < -1,\\ 2x, \, если \, -1\le x\le 1,\\ 2, \, если \, x > 1 \end{cases} \]
\(y = 2x\), если \( -1\le x\le 1\)
| \(x\) | \(-1\) | \(1\) |
| \(y\) | \(-2\) | \(2\) |

Пояснения:
Правила раскрытия модуля.
\( |x-a|= \begin{cases} x-a,\, если\, x-a\ge 0,\\ -(x-a), \, если \, x-a<0. \end{cases} \)
а) \(y=|x+2|+|x-2|\).
Нули модулей в точках \(x=-2\) и \(x=2\), поэтому выражение рассматриваем на трёх промежутках. Для \(x<-2\): оба модуля отрицательны, получаем линейную зависимость \(y=-2x\). Для \(-2\le x\le 2\): первый модуль неотрицателен, второй - отрицателен, получаем \(y=4\). Для \(x> 2\): оба vjlekz неотрицательны, получаем линейную зависимость \(y=2x\).
График состоит из двух лучей, сходящихся к горизонтальному «основанию» на уровне \(y=4\), с вершинами в точках \((-2,4)\) и \((2,4)\).
б) \(y=|x+1|-|x-1|\).
Нули модулей в \(x=-1\) и \(x=1\), поэтому выражение рассматриваем на трех промежутках. Для \(x<-1\): оба модуля отрицательны, получаем \(y=-2\). Для \(-1\le x\le 1\): первая скобка неотрицательна, вторая отрицательна, получаем линейную зависимость \(y=2x\). Для \(x > 1\): обе скобки неотрицательны, получаем \(y=2\).
В результате график — «ступенька» с горизонтальными полками \(y=-2\) слева и \(y=2\) справа, соединёнными центральным отрезком прямой \(y=2x\) между точками \((-1,-2)\) и \((1,2)\).
Вернуться к содержанию учебника