Упражнение 1050 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1050 учебника 2023-2025 (стр. 231):
С турбазы в город, отстоящий на расстоянии 24 км, вышел первый турист со скоростью 4 км/ч. Спустя 2 ч вслед за ним отправился второй турист. С какой скоростью должен идти второй турист, чтобы догнать первого до его прихода в город?
№1050 учебника 2013-2022 (стр. 237):
В таблице показано, сколько курток изготовила мастерская за каждый квартал 2004 и 2005 гг.
| Год | 2004 | |||
| Квартал | I | II | III | IV |
| Число курток | 780 | 625 | 645 | 810 |
| Год | 2005 | |||
| Квартал | I | II | III | IV |
| Число курток | 850 | 760 | 720 | 910 |
Постройте полигон, иллюстрирующий выработку мастерской в 2004 и в 2005 гг. (по кварталам). Используя полигон:
а) охарактеризуйте динамику изменения производства курток в 2004 и 2005 гг. (по кварталам);
б) укажите два квартала, следующие друг за другом, когда произошло наибольшее увеличение выработки.
Подсказка
№1050 учебника 2023-2025 (стр. 231):
Вспомните:
- Задачи на движение.
- Решение неравенств с одной переменной.
- Подобные слагаемые.
- Вычитание рациональных чисел.
- Умножение обыкновенных дробей.
- Деление рациональных чисел.
№1050 учебника 2013-2022 (стр. 237):
Вспомните, что называют полигоном.
Ответ
№1050 учебника 2023-2025 (стр. 231):
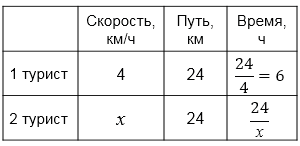
Второй турист вышел на \(2\) ч позже.
Составим неравенство:
\(\frac{24}{x} + 2 < 6\) \(/\times x\)
\(24 + 2x < 6x\)
\(2x - 6x < -24\)
\(-4x < -24\) \(/ : (-4)\)
\(x > 6\)
Ответ: скорость второго туриста должна быть более \(6\) км/ч.
Пояснения:
Обозначив скорость туриста через \(x\) км/ч (\(x > 0\)), по условию задачи составили неравенство:
\(\frac{24}{x} + 2 < 6\).
При решении неравенств используем то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства разделить или умножить на одно и то же положительное число, то получится равносильное ему неравенство;
- если обе части неравенства разделить или умножить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
№1050 учебника 2013-2022 (стр. 237):

а) Для 2004 года:
Во II квартале производство курток снизилось, в III квартале - немного повысилось, в IV квартале - значительно повысилось.
Для 2005 года:
Во II квартале производство курток снизилось, в III квартале - еще немного снизилось, в IV квартале - значительно повысилось.
б) Наибольшее увеличение выработки произошло между III и IV кварталами 2005 года.
Пояснения:
Полигон — это ломаная линия, построенная по точкам. В нашем случае по горизонтальной оси откладывают номера кварталов (последовательно: I, II, III, IV 2004 г., затем I, II, III, IV 2005 г.), а по вертикальной оси — число изготовленных курток. Каждая точка имеет координаты \((x; y)\), где \(x\) — номер квартала в порядке времени, \(y\) — выработка в этом квартале.
Чтобы описать динамику, нужно смотреть, как изменяется высота точек от квартала к кварталу, то есть растёт ли или падает ломаная линия.
Чтобы определить, два квартала, следующие друг за другом, когда произошло наибольшее увеличение выработки, нужно определить кварталы между которыми наибольшая разница между количеством курток в сторону увеличения.
Вернуться к содержанию учебника