Упражнение 134 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 54
Вернуться к содержанию учебника
Вопрос
Изобразите схематически график каждой функции (отметьте вершину параболы и направление её ветвей):
а) \(y=\frac12 x^2,\)
\(y=\frac12 x^2+4,\)
\(y=\frac12 x^2-3;\)
б) \(y=-\frac13 x^2,\)
\(y=-\frac13 x^2+2,\)
\(y=-\frac13 x^2-1;\)
в) \(y=\frac15 x^2,\)
\(y=\frac15 (x-3)^2,\)
\(y=\frac15 (x+3)^2.\)
Подсказка
Вспомните квадратичную функцию и ее график.
Ответ
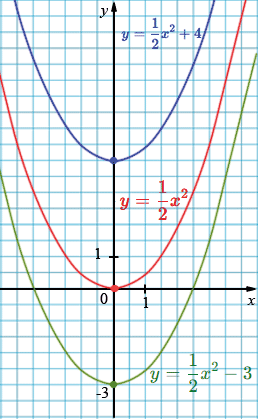
а) \( y=\tfrac12 x^2 \): вершина: \((0; 0)\), ветви вверх.
\( y=\tfrac12 x^2+4 \): вершина: \((0; 4)\), ветви вверх.
\( y=\tfrac12 x^2-3 \): вершина: \((0; -3)\), ветви вверх.
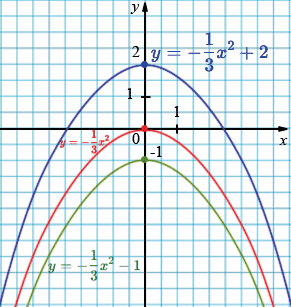
б) \( y=-\tfrac13 x^2 \): вершина: \((0; 0)\), ветви вниз.
\( y=-\tfrac13 x^2+2 \): вершина: \((0; 2)\), ветви вниз.
\( y=-\tfrac13 x^2-1 \): вершина: \((0; -1)\), ветви вниз.
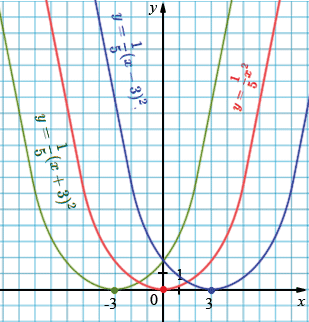
в) \( y=\tfrac15 x^2 \): вершина: \((0; 0)\), ветви вверх.
\( y=\tfrac15 (x-3)^2 \): вершина: \((3; 0)\), ветви вверх.
\( y=\tfrac15 (x+3)^2 \): вершина: \((-3; 0)\), ветви вверх.
Пояснения:
1. Формы парабол:
Формула стандартной параболы:
\( y = ax^2. \)
Если \(a>0\) — ветви вверх. Если \(a<0\) — ветви вниз.
Вершина в точке \((0; 0)\).
2. Параболы вида \(y = ax^2 + c\)
Вершина параболы сдвигается по вертикали на величину \(c\):
\( y = ax^2 + c \Rightarrow \text{вершина } (0; c). \)
3. Параболы вида \(y = a(x-h)^2\)
Вершина смещается в точку \((h; 0)\):
\( y = a(x-h)^2 \Rightarrow \text{вершина } (h;0). \)
Вернуться к содержанию учебника