Страница 39. Урок 13 - ГДЗ Математика 4 класс. Петерсон. Учебник часть 1
Страница 35. Урок 12 Страница 36. Урок 12 Страница 38. Урок 13 Страница 39. Урок 13 Страница 40. Урок 14 Страница 41. Урок 14 Страница 42. Урок 14
Вопрос
Задание № 5. Упрости выражения:
| 17 + х + 39 | у • 6 • 12 | n + 24 + 16 | 4 • m • 25 |
Подсказка
Повтори, что такое буквенные выражения.
Ответ
Решение
| 17 + х + 39 = 56 + х | n + 24 + 16 = n + 40 |
| у • 6 • 12 = у • 72 | 4 • m • 25 = 100 • m |
Пояснение
Упрощение выражения - значит уменьшение в нём количества операций, которые необходимо сделать для вычисления его значения при заданных значениях переменных.
Вопрос
Задание № 6. Построй прямоугольник со сторонами 8 см и 2 см 5 мм. Найди его периметр и площадь.
Подсказка
Повтори, что такое площадь и периметр прямоугольника.
Ответ
Вопрос
Задание № 7. Вычисли периметр и площадь многоугольника ABCDEF.
Подсказка
Повтори, что такое периметр и площадь многоугольника, а также единицу длины - дециметр.
Ответ
Решение
15 + 21 + 15 + 21 + 9 + 16 + (16 - 9) = 104 (дм)
16 • (15 + 21) - 21 • (16 - 9) = 576 - 147 = 429 (дм2)
Пояснение
Площадь прямоугольника равна произведению его длины и ширины.
Периметр прямоугольника - это сумма длин всех его сторон.
2 способ:
Площадь прямоугольника состоит из площадей двух маленьких прямоугольников. Назовём дополнительную точку - N.
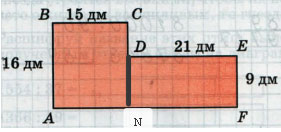
Найдём площадь прямоугольника ABCN:
16 • 15 = 240 (дм2)
Найдём площадь прямоугольника DENF:
21 • 9 = 189 (дм2)
Найдём площадь многоугольника ABCDEF:
240 + 189 = 429 (дм2)
Вопрос
Задание № 8. Александр Сергеевич Пушкин родился 6 июня 1799 года. Сколько лет и дней прошло со дня рождения Пушкина до сегодняшнего дня, включая его?
Ответ
Решение
Нужно из текущего года вычесть 1799 год и добавить количество дней, которые прошли от 6 июня.
Пояснение
Пример:
Сегодня 15 сентября 2023. От 6 июня прошло: 25 + 31 + 31 + 15 = 102 (дн.)
2023 - 1799 = 224 (г.)
Значит, со дня рождения Пушкина прошло 224 года и 102 дня.
Вопрос
Задание № 9. Пользуясь заданным алгоритмом, найди значения х, сопоставь их соответствующим буквам и расшифруй имя замечательного русского поэта.
Ответ
Решение
| а | х | |
| 4 | 40 | С |
| 20 | 60 | Б |
| 32 | 75 | И |
| 48 | 85 | В |
| 60 | 94 | Л |
| 72 | 123 | Е |
| 80 | 36 | А |
| 88 | 44 | Й |
| 92 | 48 | Р |
| 100 | 56 | О |
| 148 | 104 | Ю |
| 85 | 36 | 94 | 123 | 48 | 75 | 44 |
| В | А | Л | Е | Р | И | Й |
| 60 | 48 | 104 | 40 | 56 | 85 |
| Б | Р | Ю | С | О | В |
Пояснение
1) При а = 4:
4 : 4 = 1 > 15 - нет;
1 + 12 = 13 > 20 - нет;
13 • 5 = 65 - 25 = 40.
2) При а = 20:
20 : 4 = 5 > 15 - нет;
5 + 12 = 17 > 20 - нет;
17 • 5 = 85 - 25 = 60.
3) При а = 32:
32 : 4 = 8 > 15 - нет;
8 + 12 = 20 > 20 - нет;
20 • 5 = 100 - 25 = 75.
4) При а = 48:
48 : 4 = 12 > 15 - нет;
12 + 12 = 24 > 20 - да;
24 • 3 = 72 + 13 = 85.
5) При а = 60:
60 : 4 = 15 > 15 - нет;
15 + 12 = 27 > 20 - да;
27 • 3 = 81 + 13 = 94.
6) При а = 72:
72 : 4 = 18 > 15 - да;
18 - 9 = 9 < 10 - да;
9 • 11 = 99 + 24 = 123.
7) При а = 80:
80 : 4 = 20 > 15 - да;
20 - 9 = 11 < 10 - нет;
11 • 4 = 44 - 8 = 36.
8) При а = 88:
88 : 4 = 22 > 15 - да;
22 - 9 = 13 < 10 - нет;
13 • 4 = 52 = 8 = 44.
9) При а = 92:
92 : 4 = 23 > 15 - да;
23 - 9 = 14 < 10 - нет;
14 • 4 = 56 - 8 = 48.
10) При а = 100:
100 : 4 = 25 > 15 - да;
25 - 9 = 16 < 10 - нет;
16 • 4 = 64 - 9 = 56.
11) При а = 148:
148 : 4 = 37 > 15 - да;
37 - 9 = 28 < 10 - нет;
28 • 4 = 11 - 8 = 104.
Вопрос
Задание № 10. Найди сумму всех возможных двузначных чисел, все цифры которых нечётные.
Подсказка
Повтори нумерацию чисел.
Ответ
Решение
Выпишем все числа, у которых цифры - нечётные:
11, 13, 15, 17, 19, 31, 33, 35, 37, 39, 51, 53, 55, 57, 59, 71, 73, 75, 77, 79, 91, 93, 95, 97, 99.
Сгруппируем эти числа:
(11 + 99) + (13 + 97) + (15 + 95) + (17 + 93) + (19 + 91) + (31 + 79) + (33 + 77) + (35 + 75) + (37 + 73) + (39 + 71) + (51 + 59) + (51 + 57) + (55 + 11 + 99) = 110 + 110 + 110 + 110 + 110 + 110 + 110 + 110 + 110 + 110 + 110 + 110 + 55 = 110 • 12 + 55 = 1375
Ответ: сумма всех двузначных чисел, все цифры которых нечётные - 1375.
Пояснение
Нечетное число — это число, которое не делится на 2 без остатка.