Задание 487 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№487 учебника 2013-2022 (стр. 132):
Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 6 см. Найдите высоту, проведенную к основанию.
№487 учебника 2023-2024 (стр. 128):
 . Найдите периметр четырёхугольника, вершины которого являются серединами сторон равнобедренной трапеции.
. Найдите периметр четырёхугольника, вершины которого являются серединами сторон равнобедренной трапеции.Подсказка
№487 учебника 2013-2022 (стр. 132):
Вспомните:
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Что такое высота треугольника.
- Что такое медиана треугольника.
- Теорему Пифагора.
№487 учебника 2023-2024 (стр. 128):
Вспомните:
- Что называют равнобедренной трапецией.
- Какой четырехугольник называют параллелограммом.
- Как найти периметр многоугольника.
- Теорему Вариньона.
- Что называют средней линией треугольника, ее свойства.
Ответ
№487 учебника 2013-2022 (стр. 132):
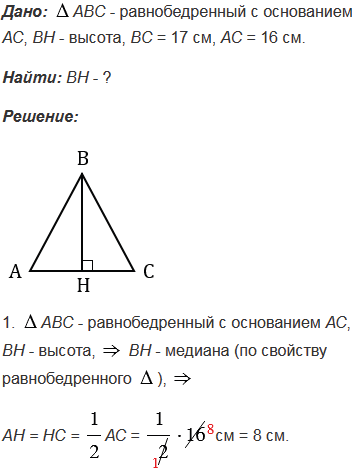


№487 учебника 2023-2024 (стр. 128):
Дано: АВСD - равнобедренная трапеция, АС = 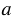 , М, N, K и Р - середины сторон АВ, ВС, СD и AD.
, М, N, K и Р - середины сторон АВ, ВС, СD и AD.
Найти: 
Решение:

1. МNKР - параллелограмм (по теореме Вариньона), 
 = 2(МN + NK).
= 2(МN + NK).
2. М и N - середины сторон АВ и ВС,  MN - средняя линия
MN - средняя линия  АВС,
АВС,  MN =
MN =  АС =
АС = 
 .
.
3. N и K - середины сторон BC и СD,  NK - средняя линия
NK - средняя линия  ВСD,
ВСD,  NK =
NK =  ВD =
ВD = 
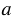 (т.к. ВD = АС - диагонали равнобедренной трапеции).
(т.к. ВD = АС - диагонали равнобедренной трапеции).
4.  = 2(
= 2(
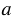 +
+ 
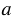 ) = 2
) = 2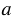 .
.
Ответ:  = 2
= 2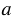 .
.
Пояснения:
Середины сторон произвольного четырёхугольника являются вершинами параллелограмма (теорема Вариньона). По условию М, N, K и Р - середины сторон АВ, ВС, СD и AD, значит, четырехугольник МNKР - параллелограмм. У параллелограмма противолежащие стороны равны, поэтому периметр параллелограмма МNKР:
 = 2(МN + NK).
= 2(МN + NK).
Средняя линия треугольника - отрезок, который соединяет середины двух его сторон. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
По условию, М и N - середины сторон АВ и ВС, следовательно, MN - средняя линия  АВС, тогда MN =
АВС, тогда MN =  АС =
АС = 
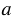 . Также N и K - середины сторон BC и СD, следовательно, NK - средняя линия
. Также N и K - середины сторон BC и СD, следовательно, NK - средняя линия  ВСD, тогда NK =
ВСD, тогда NK =  ВD =
ВD = 
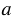 (учитываем то, что ВD = АС =
(учитываем то, что ВD = АС = 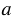 , так как диагонали равнобедренной трапеции равны).
, так как диагонали равнобедренной трапеции равны).
Итак,  = 2(МN + NK), при этом
= 2(МN + NK), при этом
MN = 
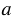 и NK =
и NK =  [img162263, тогда:
[img162263, тогда:
 = 2(
= 2(
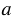 +
+ 
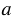 ) = 2
) = 2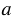 .
.
Вернуться к содержанию учебника