Упражнение 552 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

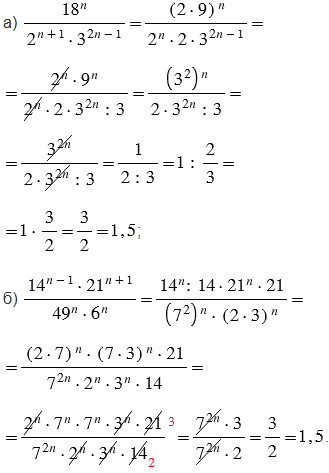
Пояснения:

Чтобы упростить выражение, используем свойства степеней:

1) при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают;

2) при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя;

3) чтобы возвести в степень произведение, достаточно возвести в эту степень каждый множитель и результаты перемножить;

4) при возведении степени в степень основание оставляют тем же, а показатели перемножают.

а) 3^4k = (3⁴)^k = 81^k - при любом значении k оканчивается единицей. Что и требовалось доказать.

б) Число 10^k состоит из единицы и k нулей, значит, число 10^k - 1 будет состоять из k девяток (10 - 1 = 9, 100 - 1 = 99, 1000 - 1 = 999 и т.д.), а число, состоящее из любого количества девяток делится нацело на 9, следовательно, число 10^k - 1 при любом значении k кратно 3. Что и требовалось доказать.