Упражнение 629 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№629 учебника 2023-2025 (стр. 136):
С помощью калькулятора найдите значение выражения 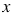 2 -
2 -  , если
, если 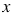 = 1,4,
= 1,4,  = 0,157.
= 0,157.
№629 учебника 2013-2022 (стр. 137):
Докажите, что выражение
\[ 2x(x-6) - 3(x^2 - 4x + 1) \]
при любых значениях \(x\) принимает отрицательные значения.
Подсказка
№629 учебника 2023-2025 (стр. 136):
Вспомните:
- Степень с натуральным показателем.
- Вычисления на калькуляторе.
№629 учебника 2013-2022 (стр. 137):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Приведение подобных слагаемых.
- Отрицательные числа.
- Сравнение рациональных чисел.
Ответ
№629 учебника 2023-2025 (стр. 136):

№629 учебника 2013-2022 (стр. 137):
\( 2x(x-6) - 3(x^2 - 4x + 1) = \)
\( = 2x^2 - 12x - 3x^2 + 12x - 3 = \)
\( = -x^2 - 3. = - (x^2 + 3)\)
Квадрат любого числа есть число не отрицательное, сумма неотрицательного числа и положительного есть число положительное, значит:
\( (x^2 + 3) > 0\).
Число противоположное любому положительному числу есть число отрицательное, значит:
\( - (x^2 + 3) < 0\), что и требовалось доказать.
Пояснения:
Раскрытие скобок по распределительному закону позволяет свести выражение к простому многочлену.
\( X(Y+Z)=XY+XZ \).
Вернуться к содержанию учебника