Упражнение 696 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 149
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№696 учебника 2023-2025 (стр. 149):
Запишите в виде многочлена выражение:
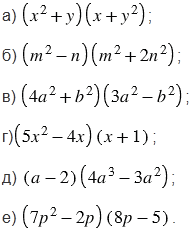
№696 учебника 2013-2022 (стр. 149):
Пусть \(a, b, c\) и \(d\) — четыре последовательных нечётных числа. Докажите, что разность \(cd - ab\) кратна 16.
Подсказка
№696 учебника 2023-2025 (стр. 149):
Вспомните:
- Что называют многочленом.
- Умножение многочлена на многочлен.
- Умножение рациональных чисел.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
№696 учебника 2013-2022 (стр. 149):
Вспомните:
- Что называют многочленом.
- Умножение многочлена на многочлен.
- Умножение рациональных чисел.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Распределительное свойство умножения.
- Делимость чисел.
Ответ
№696 учебника 2023-2025 (стр. 149):

Пояснения:
Чтобы представить выражение в виде многочлена, нужно выполнить умножение многочлена на многочлен.
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить (мы говорим об алгебраической сумме - выражение, которое можно представить в виде суммы положительных и отрицательных чисел). В решении выделены одинаковым цветом подобные слагаемые, их мы складываем (вычитаем), тем самым упрощая выражение.
Также, выполняя умножение многочлена на многочлен, помним, что при умножении степеней с одинаковыми основаниями показатели степени складывают, а основание оставляют тем же.
№696 учебника 2013-2022 (стр. 149):
Пусть \(a = 2k + 1\), тогда \(b = 2k + 3\),
\(c = 2k + 5\), \(d = 2k + 7\).
\(cd - ab = \)
\((2k+5)(2k+7) - (2k+1)(2k+3) =\)
\( = \bigl(4k^2 + 14k + 10k + 35\bigr) - \bigl(4k^2 + 6k + 2k + 3\bigr) =\)
\(=(4k^2 + 24k + 35) - (4k^2 + 8k + 3) =\)
\( = 4k^2 + 24k + 35 - 4k^2 - 8k - 3 =\)
\(=16k + 32 = 16(k + 2) \) - делится на 16.
Пояснения:
Использованные правила:
1. Общее представление нечётного числа: \(2k+1\).
2. Раскрытие произведения:
\((x+y)(u+v)=xu+xv+yu+yv\).
3. Вычитание многочленов: чтобы вычесть \((P(x) - Q(x))\), меняем знак у всех членов \(Q(x)\) и складываем с \(P(x)\).
4. Приведение подобных членов:
\(k_1X + k_2X = (k_1 + k_2)X.\)
5. Распределительное свойство умножения (вынос множителя за скобки):
\(x(y+z)=xy+xz\).
6. Критерий делимости: если число представимо в виде \(k\cdot m\), где \(m\) какой-либо многочлен, то оно кратно \(k\).
Пояснения к шагам:
- Введено общее представление для последовательных нечётных чисел через переменную \(k\).
- Раскрытие скобок и приведение подобных членов позволяют получить выражение в виде \(16k+32\).
- Вынос общего множителя 16 показывает, что разность кратна 16 по критерию делимости.
Вернуться к содержанию учебника