Упражнение 1142 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

а)  \(2x + 5y = 12\)

\( 5y = 12 - 2x \)

\(y = \frac{12 - 2x}{5} \)

\(y = \frac{12}{5} - \frac{2}{5}x \)

\(y = 2,4 - 0,4x \)

\(y = -0,4x + 2,4 \)

\(k < 0\), \(b > 0\), значит, график расположен в I, II и IV координатной четвертях.

Ответ: I, II и IV координатные четверти.

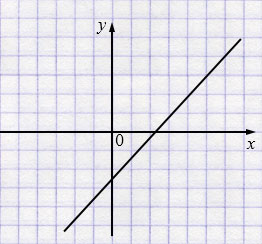
б)  \(3x - 4y = 10\)

\( -4y = 10 - 3x \)

\( y = \frac{3x - 10}{4} \)

\( y = \frac{3}{4}x - \frac{10}{4} \)

\( y = 0,75x - 2,5 \)

\(k > 0\), \(b < 0\), значит, график расположен в I, III и IV координатной четвертях.

Ответ: I, III и IV координатные четверти.

Пояснения:

Использованные приёмы:

Для каждой прямой выразили \(y\) через \(x\),то есть получили уравнение линейной функции вида \(y = kx + b\) и определили знаки коэффициентов \(k\) и \(b\), которые отвечают за расположение прямой на координатной плоскости.

Коэффициент \(k\) отвечает за возрастание (когда \(k > 0\)) или убывание (когда \(k < 0\)) линейной функции.

Коэффициент \(b\) отвечает за точку пересечения с осью \(y\), если \(b > 0\), то прямая пересекает ось \(y\) выше оси \(x\), а если \(b < 0\), то прямая пересекает ось \(y\) ниже оси \(x\).

а)

б)

\(a + b = 42\)

\(a\) и \(b\) - простые числа.

Если \(a = 2\), то

\(b = 42 - 2 = 40\) — не простое;

Если \(a = 3\), то

\(b = 42 - 3 = 39\) — не простое;

Если \(a = 5\), то

\(b = 42 - 5 = 37\) — простое.

Если \(a = 7\),

то \(b = 42 - 7 = 35\) — не простое;

Если \(a = 11\), то

\(b = 42 - 11 = 31\) — простое.

Если \(a = 13\), то

\(b = 42 - 13 = 29\) — простое.

Если \(a = 17\), то

\(b = 42 - 17 = 25\) — не простое;

Если \(a = 19\), то

\(b = 42 - 19 = 23\) — простое.

Если \(a = 23\), то

\(b = 42 - 23 = 19\) — простое.

Если \(a = 29\), то

\(b = 42 - 29 = 13\) — простое.

Если \(a = 31\), то

\(b = 42 - 31 = 11\) — простое.

Если \(a = 37\), то

\(b = 42 - 37 = 5\) — простое.

Если \(a = 41\), то

\(b = 42 - 41 = 1\) — не простое.

Ответ: \((5;37), (11;31), (13;29),\)

\((19;23), (23;19), (29;13),\)

\((31;11), (37;5)\).

Пояснения:

– Простое число — натуральное число, имеющее ровно два делителя: 1 и само себя.

– Мы их исходного уравнения выразили \(b\) и проверили, является ли \(b\) простым при каждом простом \(a\).