Упражнение 176 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

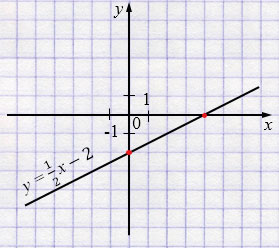
а) \(y=\frac12x-2\)

1) Пересечение с осью \(y\) при \(x=0\):

\( y=\frac12\cdot0-2=-2. \)

Точка \((0;\,-2)\).

2) Пересечение с осью \(x\) при \(y=0\):

\( 0=\tfrac12x-2 \)

\(\tfrac12x=2\)    /\(\times2\)

\(x=4. \)

Точка \((4;\,0)\).

б) \(y=-0,4x+2\)

1) Пересечение с осью \(y\) при \(x=0\):

\( y=-0,4\cdot0+2=2. \)

Точка \((0;\,2)\).

2) Пересечение с осью \(x\) при \(y=0\):

\( 0=-0,4x+2\)

\(0,4x=2\)

\(x=\frac{2}{0,4}\)

\(x=\frac{20}{4}\)

\(x=5. \)

Точка \((5;\,0)\).

Пояснения:

Использованные правила и приёмы:

• Координата пересечения с осью \(y\) находится при \(x=0\).

• Координата пересечения с осью \(x\) находится при \(y=0\).

• Для построения графика прямой достаточно двух точек, которые мы определили.

В каждом случае сначала подставили \(x=0\) для получения точки пересечения с осью \(y\), затем подставили \(y=0\) и решили уравнение для \(x\) для точки пересечения с осью \(x\). График проводим через найденные точки.

а) \(k>0,\;b>0\)

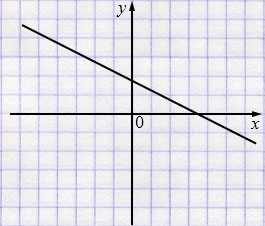
б) \(k<0,\;b>0\)

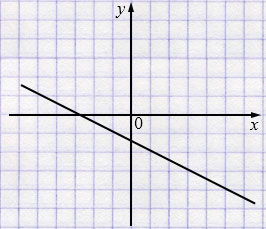
в) \(k<0,\;b<0\)

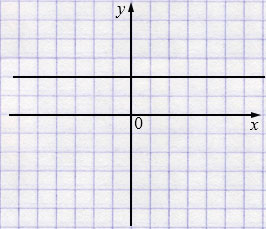
г) \(k=0,\;b>0\)

Пояснения:

а) \(k>0,\;b>0\) - прямая возрастающая и пересекающая ось \(y\) выше оси \(x\).

б) \(k<0,\;b>0\) - прямая убывающая и пересекающая ось \(y\) выше оси \(x\).

в) \(k<0,\;b<0\) - прямая убывающая и пересекающая ось \(y\) ниже оси \(x\).

г) \(k=0,\;b>0\) - прямая параллельная оси \(x\) и пересекающая ось \(y\) выше оси \(x\).