Упражнение 256 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№256 учебника 2023-2025 (стр. 62):
Докажите, что если \(z\) является средним гармоническим положительных чисел \(a\) и \(b\), причём \(a\neq b\), то справедливо равенство
\[ \frac{1}{z - a} \;+\;\frac{1}{z - b} \;=\; \frac{1}{a} + \frac{1}{b}. \]
№256 учебника 2013-2022 (стр. 59):
Найдите область определения функции и постройте её график:
а) \(y = \dfrac{36}{(x+1)^2 - (x-1)^2}\);
б) \(y = \dfrac{18 - 12x}{x^2 - 3x} - \dfrac{6}{3 - x}\);
в) \(y = \dfrac{16}{(2 - x)^2 - (2 + x)^2}\);
г) \(y = \dfrac{3x(x+1) - 3x^2 + 15}{x(x+5)}\).
Подсказка
№256 учебника 2023-2025 (стр. 62):
№256 учебника 2013-2022 (стр. 59):
Ответ
№256 учебника 2023-2025 (стр. 62):
\( z = \frac{2}{\frac1a + \frac1b} = \frac{2ab}{a+b}. \)
\( \frac{1}{z - a} \;+\;\frac{1}{z - b} =\)
\(= \frac{1}{ \frac{2ab}{a+b} - a} + \frac{1}{\frac{2ab}{a+b} - b } =\)
\(= \frac{1}{\frac{2ab - a(a+b)}{a+b} } + \frac{1}{\frac{2ab - b(a+b)}{a+b} } =\)
\( =\frac{1}{\frac{ab - a^2}{a+b}} \;+\;\frac{1}{\frac{ab - b^2}{a+b}} =\)
\(= \frac{1}{-\dfrac{a(a - b)}{a+b}} \;+\; \frac{1}{\dfrac{b(a - b)}{a+b}} =\)
\(= -\,\frac{a+b}{a(a - b)} \;+\; \frac{a+b}{b(a - b)} =\)
\(= \frac{a+b}{a - b}\Bigl(-\frac{1}{a}^{\color{red}{\backslash{b}}} + \frac{1}{b}^{\color{red}{\backslash{a}}}\Bigr) =\)
\(=\frac{a+b}{a - b}\;\cdot\frac{-b + a}{ab} = \frac{a+b}{ab} \)
\(= \frac{1}{a} + \frac{1}{b} \)
\(\frac{1}{a} + \frac{1}{b} = \frac{1}{a} + \frac{1}{b} \) - верно.
Пояснения:
• Среднее гармоническое \(a_{ср.}\) для \(n\) чисел \(a_1, a_2,\dots,a_n\) определяется как
\( a_{ср.} =\frac{n}{\frac{1}{a_1} + \frac{1}{a_2}+\dots+ \frac{1}{a_n}}.\)
Тогда среднее гармоническое двух чисел \(a,b\): \(\;z = \dfrac{2}{\frac1a+\frac1b} = \dfrac{2ab}{a+b}\).
• Для вычисления суммы обратных дробей приводим их к общему знаменателю, складываем числители и упрощаем.
• Противоположные выражения:
\(\;b - a = -(a - b)\).
• Вынесение общего множителя за скобки:
\(\;\frac{(a+b)}{(a-b)}\)
• Сложение дробей с разными знаменателями:
\(-\frac1a +\frac1b = \frac{-b+a}{ab}\).
Благодаря этим преобразованиям получаем тождество.
№256 учебника 2013-2022 (стр. 59):
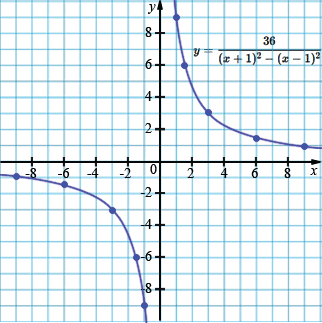
а) \(y = \dfrac{36}{(x+1)^2 - (x-1)^2}\);
\((x+1)^2 - (x-1)^2 \neq0\)
\(x^2 +2x+1 - (x^2 -2x+1) \neq0\)
\( 4x\neq0\)
\(x\neq0\)
Область определения: все числа кроме \(0\).
\(y = \dfrac{36}{4x} = \dfrac{9}{x},\quad x \neq 0\)
| \(x\) | -9 | -6 | -3 | -1,5 | -1 |
| \(y\) | -1 | -1,5 | -3 | -6 | -9 |
| \(x\) | 1 | 1,5 | 3 | 6 | 9 |
| \(y\) | 9 | 6 | 3 | 1,5 | 1 |
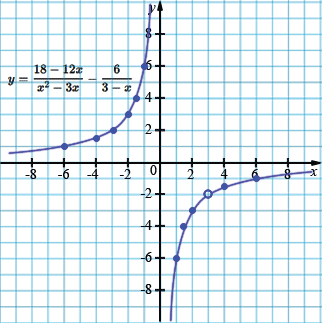
б) \(y = \dfrac{18 - 12x}{x^2 - 3x} - \dfrac{6}{3 - x}\);
\(x^2 - 3x \neq0\) \(3-x\neq0\)
\(x(x-3)\neq0\) \(x\neq3\)
\(x\neq0\) \(x-3\neq0\)
\(x\neq3\)
Область определения: все числа кроме \(3; 0\).
\(y=\dfrac{18 -12x}{x(x-3)} - \dfrac{6}{3-x} =\)
\(=\dfrac{18 -12x}{x(x-3)} + \dfrac{6}{x-3}=\)
\(=\dfrac{18 -12x +6x}{x(x-3)} = \dfrac{18 -6x}{x(x-3)} =\)
\(=\dfrac{6(3-x)}{x(x-3)} = -\dfrac{6}{x},\quad x\neq 0,\,3\)
| \(x\) | 6 | 4 | 3 | 2 | 1,5 | 1 |
| \(y\) | -1 | -1,5 | -2 | -3 | -4 | -6 |
| \(x\) | -6 | -4 | -3 | -2 | -1,5 | -1 |
| \(y\) | 1 | 1,5 | 2 | 3 | 4 | 6 |
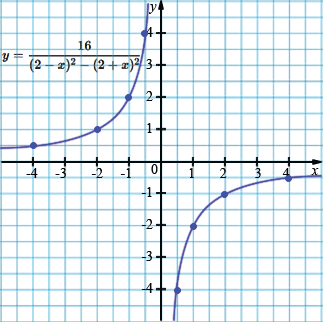
в) \(y = \dfrac{16}{(2 - x)^2 - (2 + x)^2}\);
\((2 - x)^2 - (2 + x)^2 \neq0\)
\( (4 -4x + x^2) - (4 +4x + x^2) \neq0\)
\(-8x\neq0\)
\(x\neq0\)
\(y = \dfrac{16}{(2 - x)^2 - (2 + x)^2}=\)
\(=\dfrac{16}{-8x} = -\dfrac{2}{x},\quad x\neq 0\)
| \(x\) | -4 | -2 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 |
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | -4 | -2 | -1 | -0,5 |
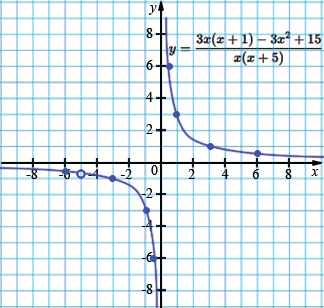
г) \(y = \dfrac{3x(x+1) - 3x^2 + 15}{x(x+5)}\).
\(x(x+5)\neq0\)
\(x\neq0\) \(x+5\neq0\)
\(x\neq-5\)
Область определения: все числа кроме \(0\) и \(-5\).
\(y = \dfrac{3x(x+1) - 3x^2 + 15}{x(x+5)}=\)
\(= \dfrac{3x^2 +3x -3x^2 +15}{x(x+5)}=\)
\(= \dfrac{3(x+5}{x(x+5)}=\dfrac{3}{x},\) \( x\neq 0,\,-5\)
| \(x\) | -6 | -5 | -3 | -1 | -0,5 |
| \(y\) | -0,5 | -0,6 | -1 | -3 | -6 |
| \(x\) | 0,5 | 1 | 3 | 6 |
| \(y\) | 6 | 3 | 1 | 0,5 |
Пояснения:
Использованные правила и формулы:
Разность квадратов двух выражений:
\(a^2 - b^2 = (a - b)(a + b)\)
Правило приведения дробей к общему знаменателю и сокращения множителей.
Для каждого выражения область определения находится из условия ненулевого знаменателя.
В пункте а) мы применили формулу разности квадратов, чтобы свести сложный квадрат к простому множителю \(4x\), после чего получили функцию \(y=\frac{9}{x}\).
В пункте б) мы раскладываем \(x^2-3x\) в множители, затем приводим дроби к общему знаменателю и сокращаем общий множитель \((x-3)\), получая \(y=-\frac{6}{x}\). Замечаем, что в исходном выражении была особая точка при \(x=3\), которая будет "выколота" в графике исходной функции.
В пункте в) снова используем разность квадратов, получая знаменатель \(-8x\) и функцию \(y=-\frac{2}{x}\).
В пункте г) упрощаем числитель: \(3x(x+1)-3x^2+15 = 3(x+5)\), сокращаем с \((x+5)\) в знаменателе и получаем \(y=\frac{3}{x}\), помня о разрывах при \(x=0\) и \(x=-5\).
Графики всех функций представляют собой гиперболы вида \(y=\frac{A}{x}\). В пунктах б) и г) существуют дополнительные «разрывы» в точках, где сокращались множители.
Вернуться к содержанию учебника