Упражнение 261 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№261 учебника 2023-2025 (стр. 62):
Постройте график функции \[y = -4 \;-\;\frac{x+2}{x^2 + 2x}.\] Определите, при каких значениях \(m\) прямая \(y = m\) не имеет с графиком общих точек.
№261 учебника 2013-2022 (стр. 60):
Могут ли графики функций
\(y = \frac{k}{x}\quad(k\neq0)\) и \(y = ax + b\)
пересекаться:
а) только в одной точке;
б) только в двух точках;
в) в трёх точках?
Подсказка
№261 учебника 2023-2025 (стр. 62):
№261 учебника 2013-2022 (стр. 60):
Ответ
№261 учебника 2023-2025 (стр. 62):
\(y = -4 \;-\;\frac{x+2}{x^2 + 2x}\)
Область определения:
\(x^2+2x \neq0\)
\(x(x+2)\neq 0\)
\(x\neq0\) \(x+2\neq0\)
\(x\neq-2\)
\(y = -4 \;-\;\frac{x+2}{x^2 + 2x}=\)
\(= -4 \;-\;\frac{x+2}{x(x + 2)}=-4 \;-\;\frac{1}{x},\)
\( x\neq 0,\,-2.\)
| \(x\) | 0,25 | 0,5 | 1 | 2 | 4 |
| \(y\) | -8 | -6 | -5 | -4,5 | -4,25 |
| \(x\) | -0,25 | -0,5 | -1 | -2 | -4 |
| \(y\) | 0 | -2 | -3 | -3,5 | -3,75 |

Пересечений нет при:
\(m = -4 \quad\text{и}\quad m = -3,5.\)
Пояснения:
1. Упрощение дроби:
Использована разложение на множители:
\[x^2+2x = x(x+2),\]
и сокращение одинаковых множителей.
Область определения: все числа кроме \(0,\,-2.\)
После упрощения выражения получили функцию \(y-=-4 \;-\;\frac{1}{x}.\) Графиком данной функции является гипербола, которая смещенна ниже оси абсцысс на 4 единичных отрезков. Заметим, что так как исходная функция не определена в точке с абсциссой \(-2\), то точка \((-2; 3,5)\) на графике будет "выколотой".
№261 учебника 2013-2022 (стр. 60):
1 вариант решения:
\(y = \frac{k}{x}\quad(k\neq0)\) - графиком является гипербола.
\(y = ax + b\) - графиком является прямая.
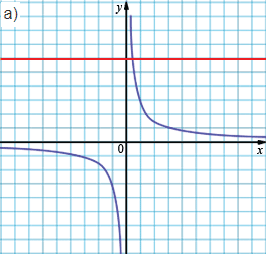
могут пересекаться только в 1 точке.
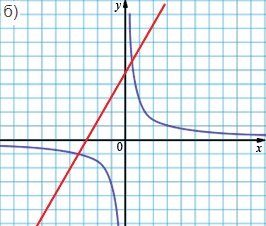
могут пересекаться только в 2 точках.
в) не могут пересекаться в 3 точках.
2 вариант решения:
Для нахождения точек пересечения решим уравнение
\(\frac{k}{x} = ax + b,\quad x\neq0\ \) \(|\times x\)
\(k = ax^2 + bx\)
\[ax^2 + bx - k = 0\]
\(D = b^2 + 4ak.\)
а) Пересечение в одной точке возможно, если \(D = 0.\)
Так как квадратное уравнение имеет единственный действительный корень.
б) Пересечение в двух точках происходит, если \(D > 0.\)
Так как квадратное уравнение имеет два различных действительных корня.
в) Пересечение в трёх точках невозможно, поскольку квадратное уравнение не может иметь более двух корней.
Пояснения:
1. Переход к квадратному уравнению:
Приравнивание \(\frac{k}{x}\) и \(ax+b\) и домножение на \(x\neq0\) дают уравнение второй степени.
2. Дискриминант и число решений:
Формула для дискриминанта:
\(D = B^2 - 4AC\), где \(A=a\), \(B=b\), \(C=-k\).
Тогда:
\(D = b^2 - 4\cdot a\cdot(-k) = b^2 + 4ak.\)
Если \(D>0\), два пересечения; \(D=0\), одно (касательная); \(D<0\), нет пересечений.
Вернуться к содержанию учебника