Упражнение 262 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№262 учебника 2023-2025 (стр. 62):
Постройте график функции:
а) \(y=\dfrac{4}{|x|}\);
б) \(y=\dfrac{2{,}4}{|x|}\);
в) \(y=\dfrac{1}{|x|}\);
г) \(y=\dfrac{-1}{|x|}\);
д) \(y=-\dfrac{6}{|x|}\);
е) \(y=\dfrac{-3{,}6}{|x|}\).
№262 учебника 2013-2022 (стр. 60):
Могут ли графики функций \(y = \frac{k}{x}\) и \(y = a x + b\) пересекаться в двух точках, лежащих:
а) в одной четверти;
б) в первой и второй четвертях;
в) в первой и третьей четвертях?
Подсказка
№262 учебника 2023-2025 (стр. 62):
№262 учебника 2013-2022 (стр. 60):
Ответ
№262 учебника 2023-2025 (стр. 62):
а) \(y=\dfrac{4}{|x|}\);
Область определения: \(x\neq0\).
\(y=\dfrac{4}{|x|}= \begin{cases}\dfrac{4}{x}, & x>0,\\ -\,\dfrac{4}{x}, & x<0. \end{cases}\)
| \(x\) | -8 | -4 | -2 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 | 8 |
| \(x\) | 8 | 4 | 2 | 1 | 0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 | 8 |

б) \(y=\dfrac{2{,}4}{|x|}\);
Область определения: \(x\neq0\).
\(y=\dfrac{2{,}4}{|x|}= \begin{cases}\dfrac{2,4}{x}, & x>0,\\ -\,\dfrac{2,4}{x}, & x<0. \end{cases}\)
| \(x\) | -8 | -3 | -2,4 | -1 | -0,8 | -0,3 |
| \(y\) | 0,3 | 0,8 | 1 | 2,4 | 3 | 8 |
| \(x\) | 8 | 3 | 2,4 | 1 | 0,8 | 0,3 |
| \(y\) | 0,3 | 0,8 | 1 | 2,4 | 3 | 8 |

в) \(y=\dfrac{1}{|x|}\);
Область определения: \(x\neq0\).
\(y=\dfrac{1}{|x|}= \begin{cases}\dfrac{1}{x}, & x>0,\\ -\,\dfrac{1}{x}, & x<0. \end{cases}\)
| \(x\) | -0,25 | -0,5 | -1 | -2 | -4 |
| \(y\) | 4 | 2 | 1 | -0,5 | 0,25 |
| \(x\) | 4 | 2 | 1 | 0,5 | 0,25 |
| \(y\) | 0,25 | 0,5 | 1 | 2 | 4 |

г) \(y=\dfrac{-1}{|x|}\);
Область определения: \(x\neq0\).
\(y=\dfrac{-1}{|x|}= \begin{cases}-\dfrac{1}{x}, & x>0,\\ \,\dfrac{1}{x}, & x<0. \end{cases}\)
| \(x\) | -0,25 | -0,5 | -1 | -2 | -4 |
| \(y\) | -4 | -2 | -1 | -0,5 | -0,25 |
| \(x\) | 0,25 | 0,5 | 1 | 2 | 4 |
| \(y\) | -4 | -2 | -1 | -0,5 | -0,25 |

д) \(y=-\dfrac{6}{|x|}\);
Область определения: \(x\neq0\).
\(y=-\dfrac{6}{|x|}= \begin{cases}-\dfrac{6}{x}, & x>0,\\ \,\dfrac{6}{x}, & x<0. \end{cases}\)
| \(x\) | -6 | -4 | -3 | -2 | -1,5 | -1 |
| \(y\) | -1 | -1,5 | -2 | -3 | -4 | -6 |
| \(x\) | 6 | 4 | 3 | 2 | 1,5 | 1 |
| \(y\) | -1 | -1,5 | -2 | -3 | -4 | -6 |

е) \(y=\dfrac{-3{,}6}{|x|}\).
Область определения: \(x\neq0\).
\(y=\dfrac{-3,6}{|x|}= \begin{cases}-\dfrac{3,6}{x}, & x>0,\\ \\ \,\dfrac{3,6}{x}, & x<0. \end{cases}\)
| \(x\) | -6 | -4 | -3 | -2 | -1 | -0,6 |
| \(y\) | -0,6 | -0,9 | -1,2 | -1,8 | -3,6 | -6 |
| \(x\) | 6 | 4 | 3 | 2 | 1 | 0,6 |
| \(y\) | -0,6 | -0,9 | -1,2 | -1,8 | -3,6 | -6 |

Пояснения:
Графики всех функций представляют собой две ветви гиперболы. Коэффициент в числителе растягивает или сжимает график вдоль оси \(Oy\), знак определяет, располагаются ли ветви в верхней (\(y>0\)) или нижней (\(y<0\)) полуплоскости.
Модуль:
\[\displaystyle |x| = \begin{cases} x, & x>0,\\ -\,x, & x<0. \end{cases}\]
Поэтому дробь \(\frac{k}{|x|}\) задаёт разные правила для \(x>0\) и \(x<0\).
№262 учебника 2013-2022 (стр. 60):
\(y = \frac{k}{x}\quad(k\neq 0)\) - графиком является гипербола.
\(y = a x + b\) - графиком является прямая.
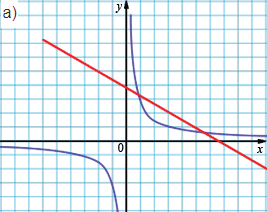
Могут пересекаться в двух точках, лежащих в одной четверти.
б) Не могут пересекаться в первой и во второй четвертях, так как ветви гиперболы находятся либо в первой и третьей четвертях, либо во второй и четвертой четвертях.
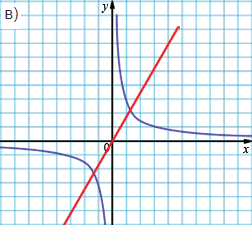
Могут пересекаться в двух точках, лежащих в первой и в третьей четвертях.
Вернуться к содержанию учебника