Упражнение 267 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№267 учебника 2023-2025 (стр. 63):
Могут ли графики функций \(y = \frac{k}{x}\quad(k\neq 0)\) и \(y = a x + b\) пересекаться в двух точках, лежащих:
а) в одной четверти;
б) в первой и второй четвертях;
в) в первой и третьей четвертях?
№267 учебника 2013-2022 (стр. 65):
Представьте в виде бесконечной десятичной дроби число:
а) \(\dfrac{1}{3}\); б) \(\dfrac{5}{6}\); в) \(\dfrac{1}{7}\);
г) \(-\dfrac{20}{9}\); д) \(-\dfrac{8}{15}\); е) \(10{,}28\);
ж) \(-17\); з) \(\dfrac{3}{16}\); и) \(-1\dfrac{3}{40}\); к) \(2\dfrac{7}{11}\).
Подсказка
№267 учебника 2023-2025 (стр. 63):
№267 учебника 2013-2022 (стр. 65):
Вспомните:
Ответ
№267 учебника 2023-2025 (стр. 63):
\(y = \frac{k}{x}\quad(k\neq 0)\) - графиком является гипербола.
\(y = a x + b\) - графиком является прямая.
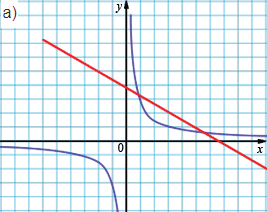
Могут пересекаться в двух точках, лежащих в одной четверти.
б) Не могут пересекаться в первой и во второй четвертях, так как ветви гиперболы находятся либо в первой и третьей четвертях, либо во второй и четвертой четвертях.
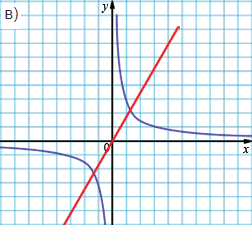
Могут пересекаться в двух точках, лежащих в первой и в третьей четвертях.
№267 учебника 2013-2022 (стр. 65):
а) \(\dfrac{1}{3} = 0{,}(3)\)
| - | 1 | 3 | |||||||||||||
| 9 | 0 | , | 3 | 3 | 3 | . | . | . | |||||||
| - | 1 | 0 | |||||||||||||
| 9 | |||||||||||||||
| - | 1 | 0 | |||||||||||||
| 9 | |||||||||||||||
| 1 |
б) \(\dfrac{5}{6} = 0{,}8(3)\)
| - | 5 | 6 | ||||||||||||||
| 4 | 8 | 0 | , | 8 | 3 | 3 | 3 | . | . | . | ||||||
| - | 2 | 0 | ||||||||||||||
| 1 | 8 | |||||||||||||||
| - | 2 | 0 | ||||||||||||||
| 1 | 8 | |||||||||||||||
| - | 2 | 0 | ||||||||||||||
| 1 | 8 | |||||||||||||||
| 2 |
в) \(\dfrac{1}{7} = 0{,}(142857)\)
| - | 1 | 7 | |||||||||||||||||
| 7 | 0 | , | 1 | 4 | 2 | 8 | 5 | 7 | 1 | . | . | . | |||||||
| - | 3 | 0 | |||||||||||||||||
| 2 | 8 | ||||||||||||||||||
| - | 2 | 0 | |||||||||||||||||
| 1 | 4 | ||||||||||||||||||
| - | 6 | 0 | |||||||||||||||||
| 5 | 6 | ||||||||||||||||||
| - | 4 | 0 | |||||||||||||||||
| 3 | 5 | ||||||||||||||||||
| - | 5 | 0 | |||||||||||||||||
| 4 | 9 | ||||||||||||||||||
| - | 1 | 0 | |||||||||||||||||
| 7 | |||||||||||||||||||
| 3 |
г) \(-\dfrac{20}{9} = -2{,}(2)\)
| - | 2 | 0 | 9 | |||||||||||||
| 1 | 8 | 2 | , | 2 | 2 | 2 | . | . | . | |||||||
| - | 2 | 0 | ||||||||||||||
| 1 | 8 | |||||||||||||||
| - | 2 | 0 | ||||||||||||||
| 1 | 8 | |||||||||||||||
| - | 2 | 0 | ||||||||||||||
| 1 | 8 | |||||||||||||||
| 2 |
д) \(-\dfrac{8}{15} = -0{,}5(3)\)
| - | 8 | 1 | 5 | |||||||||||||
| 7 | 5 | 0 | , | 5 | 3 | 3 | 3 | . | . | . | ||||||
| - | 5 | 0 | ||||||||||||||
| 4 | 5 | |||||||||||||||
| - | 5 | 0 | ||||||||||||||
| 4 | 5 | |||||||||||||||
| - | 5 | 0 | ||||||||||||||
| 4 | 5 | |||||||||||||||
| 5 |
е) \(10{,}28 = 10{,}28(0)\)
ж) \(-17 = -17{,}(0)\)
з) \(\dfrac{3}{16} = 0{,}1875(0)\)
и) \(-1\dfrac{3}{40} = -\dfrac{43}{40} = -1{,}075(0)\)
к) \(2\dfrac{7}{11} = \dfrac{29}{11} = 2{,}(63)\)
| - | 2 | 9 | 1 | 1 | |||||||||||||
| 2 | 2 | 2 | , | 6 | 3 | 6 | 3 | . | . | . | |||||||
| - | 7 | 0 | |||||||||||||||
| 6 | 6 | ||||||||||||||||
| - | 4 | 0 | |||||||||||||||
| 3 | 3 | ||||||||||||||||
| - | 7 | 0 | |||||||||||||||
| 6 | 6 | ||||||||||||||||
| 4 |
Пояснения:
Любое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби.
Если знаменатель в несократимой дроби имеет только множители 2 и 5, дробь конечная; если другие простые множители — дробь бесконечная периодическая.
Вернуться к содержанию учебника