Упражнение 755 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

Пусть два последовательных натуральных числа:

\( n,\; n+1 \).

Составим уравнение:

\( (n+(n+1))^2=n^2+(n+1)^2+112 \)

\( (2n+1)^2=n^2+n^2+2n+1+112 \)

\( 4n^2+4n+1=2n^2+2n+113 \)

\( 4n^2+4n+1-2n^2-2n-113=0 \)

\( 2n^2+2n-112=0 \)     \(/ : 2\)

\( n^2+n-56=0 \)

\(a = 1\),  \(b = 1\),  \(c = -56\)

\( D=b^2 - 4ac=1^2-4\cdot 1\cdot (-56)=\)

\(=1+224=225 \),     \(\sqrt D = 15\).

\(n_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( n_1=\frac{-1+ 15}{2\cdot1}=\frac{14}{2}=7\).

\(n_2=\frac{-1- 15}{2\cdot1}=\frac{-16}{2}=-8 \) - не удовлетворяет условию.

\(7\) - первое число.

\(8\) - второе число.

Ответ: числа: \(7\) и \(8\).

Пояснения:

Вводим обозначения для двух последовательных натуральных чисел и составляем уравнение. Раскрываем скобки по формуле квадрата суммы:

\((a +b)^2 = a^2 + 2ab + b^2\).

Затем приводим подобные и получаем полное квадратное уравнение, которое имеет два корня. Отрицательный корень не подходит, так как по условию числа должны быть натуральными.

\(a > b \), тогда \( \dfrac{1}{a} < \dfrac{1}{b}\).

\(d < b\), тогда \( \dfrac{1}{d} > \dfrac{1}{b}\).

\(c > a \), тогда \( \dfrac{1}{c} < \dfrac{1}{a}\).

\(\dfrac{1}{c} < \dfrac{1}{a} < \dfrac{1}{b} < \dfrac{1}{d}\).

Пояснения:

Используем свойство обратных величин: если \(x\) и \(y\) - положительные числа и \(x < y\), то \(\dfrac{1}{x} > \dfrac{1}{y}\).

\(a > b\), \(d < b\), \(c > a\)

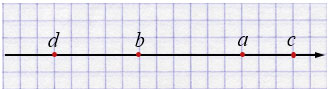
\(d < b < a < c\)

\(\dfrac{1}{c} < \dfrac{1}{a} < \dfrac{1}{b} < \dfrac{1}{d}\).