Упражнение 859 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \( \frac{5}{x} = 2 - \frac{3}{x-2}\)    \(/\times x(x-2)\)

ОДЗ: \(x\ne0\)  и  \(x-2 \neq0\)

                          \(x\ne2\).

\(5(x-2)=2x(x-2) - 3x\)

\(5x -10 = 2x^2 - 4x - 3x \)

\(5x -10 = 2x^2 -7x \)

\(2x^2 - 7x - 5x +10 = 0\)

\(2x^2 -12x +10 = 0\)   \( /: 2\)

\( x^2 - 6x + 5 = 0\)

\(a=1\),  \(b = -6\),  \(c = 5\)

\(D = b^2 - 4ac = (-6)^2-4\cdot1\cdot5 =\)

\(=36 -20 = 16\),   \(\sqrt D = 4\)

\(x_1 = \frac{-(-6)+ 4}{2\cdot1} = \frac{10}{2}=5\).

\(x_2 = \frac{-(-6)- 4}{2\cdot1} = \frac{2}{2}=1\).

 Ответ: \(1;  5\).

б) \( \frac{3}{2x-1} = 5x - 9\)    \(/\times (2x-1)\)

ОДЗ: \(2x - 1 \neq0\)

         \(2x \neq 1\)

         \(x \neq \frac{1}{2}\)

\( 3 = (5x-9)(2x-1)\)

\(3 = 10x^2 - 5x - 18x + 9\)

\( 3 = 10x^2 - 23x + 9\)

\( 10x^2 - 23x + 9 - 3 = 0\)

\( 10x^2 - 23x + 6 = 0\)

\(D =b^2-4ac=\)

\(=(-23)^2 - 4 \cdot 10 \cdot 6 =\)

\(=529 - 240 = 289\),   \( \sqrt{D} = 17\).

\( x_1 = \frac{-(-23) + 17}{2\cdot10}=\frac{40}{20} = 2\).

\( x_2 = \frac{-(-23) - 17}{2\cdot10}= \frac{6}{20} =\)

\(=\frac{3}{10} = 0,3\).

Ответ: \(\frac{3}{10};   2\).

Пояснения:

Алгоритм решения дробных рациональных уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

Решение целых уравнений:

1) Полное квадратное уравнение \(ax^2 + bx + c=0\), которое решается через дискриминант \(D = b^2-4ac\).

– если \(D>0\), то уравнение имеет два корня:

\(x_1 =\frac{-b+\sqrt{D}}{2a}\);

\(x_2 =\frac{-b-\sqrt{D}}{2a}\).

2) Линейное уравнение вида \(ax = b\), которое при \(a\neq0\) имеет единственный корень \(x = \frac{a}{b}\).

Раскрытие скобок:

\(a(b + c) = ab + ac\);

\((a + b)(c -d) = ac - ad + bc -bd\).

а) \(\sqrt{2x - 4}\)

\(2x - 4 \geqslant 0\)

\(2x \geqslant 4\)    \(/ : 2\)

\(x \geqslant 2\)

Ответ: \([2; +\infty)\).

б) \(\sqrt{4 - 6a}\)

\(4 - 6a \geqslant 0\)

\(-6a \geqslant -4\)      \(/ : (-6)\)

\(a \leqslant \dfrac{4}{6}\)

\(a \leqslant \dfrac{2}{3}\)

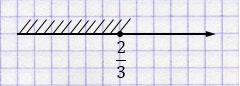
Ответ: \((-\infty; \dfrac{2}{3}]\).

в) \(\sqrt{\dfrac{1+3a}{25}}\)

\(\dfrac{1+3a}{25} \geqslant 0\)   \(/\times 25\)

\(1+3a \geqslant 0\)

\(3a \geqslant -1\)  \(/ : 3\)

\(a \geqslant -\dfrac{1}{3}\)

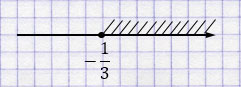
Ответ: \([-\dfrac{1}{3}; +\infty)\).

г) \(\sqrt{\dfrac{7 - 5a}{8}}\)

\(\dfrac{7 - 5a}{8} \geqslant 0\)   \(/\times 8\)

\(7 - 5a \geqslant 0\)

\(- 5a \geqslant -7\)   \(/ : -5\)

\(a \leqslant \dfrac{7}{5}\)

\(a \leqslant 1,4\)

Ответ: \((-\infty; 1,4]\).

д) \(\sqrt{-3(1-5x)}\)

\(-3(1-5x) \geqslant 0\)

\(-3 + 15x \geqslant 0\)

\(15x \geqslant 3\)   \(/ :15\)

\(x \geqslant \dfrac{3}{15}\)

\(x \geqslant \dfrac{1}{5}\)

\(x \geqslant 0,2\)

Ответ: \([0,2; +\infty)\).

е) \(\sqrt{-(6-x)}\)

\(-(6-x) \geqslant 0\)

\(-6 + x \geqslant 0\)

\(x \geqslant 6\)

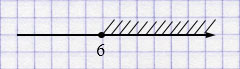
Ответ: \([6; +\infty)\).

Пояснения:

Подкоренное выражение в квадратном корне должно быть неотрицательным число, то есть \(\geqslant 0\), исходя из этого условия в каждом случае составляем неравенства и решаем их.

В пунктах в) и г) при решении неравенств сначала избавляемся от знаменателей, на знаменатель дроби, входящей в неравенство, учитывая то, что если обе части неравенства умножить на одно и то же положительное число, то получится равносильное ему неравенство.

В пунктах д) и е) при решении неравенств сначала раскрываем скобки, учитывая то, что знак минус перед скобками при их раскрытии меняет все знаки в скобках на противоположные.

Затем при решении неравенств используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.