Упражнение 992 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(-6{,}5<\dfrac{7x+6}{2}\le 20{,}5 \)

\(\begin{cases} \dfrac{7x+6}{2} > -6,5,  /\times 2 \\[2pt] \dfrac{7x+6}{2}\le 20{,}5    /\times 2 \end{cases} \)

\(\begin{cases} 7x+6 > -13,\\ 7x+6\le 41 \end{cases}\)

\(\begin{cases} 7x > -13 - 6,\\ 7x\le 41 -6 \end{cases}\)

\(\begin{cases} 7x > -19, / : 7 \\ 7x\le 35 / : 7 \end{cases} \)

\(\begin{cases} x > -\frac{19}{7}, \\ x\le 5 \end{cases} \)

\(\begin{cases} x > -2\frac{5}{7}, \\ x\le 5 \end{cases} \)

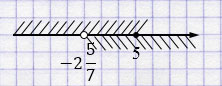
Ответ: \((-2\frac{5}{7}; 5]\), целые числа:

\(-2,\;0,\;5\).

б) \(-1<\dfrac{4-a}{3}\le 5\)

\(\begin{cases} \dfrac{4-a}{3}> -1,  /\times 3 \\ \dfrac{4-a}{3}\le 5  /\times 3 \end{cases} \)

\(\begin{cases} 4-a > -3,\\ 4-a\le 15 \end{cases} \)

\(\begin{cases} -a > -3-4,\\ -a\le 15-4 \end{cases} \)

\(\begin{cases} -a > -7, /\times (-1) \\ -a\le 11  /\times (-1) \end{cases} \)

\(\begin{cases} a <7, \\ a\ge -11 \end{cases} \)

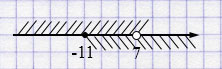
Ответ: \([-11,\,7)\), целые числа:

\(-10,\;0,\;6\).

в) \(-2\le\dfrac{3x-1}{8}\le 0 \)

\(\begin{cases}  \dfrac{3x-1}{8} \ge -2, /\times 8 \\ \dfrac{3x-1}{8}\le 0 \end{cases} \)

\(\begin{cases}  3x-1 \ge -16,\\ 3x-1\le 0 \end{cases} \)

\(\begin{cases}  3x \ge -16+1, \\ 3x\le 1\end{cases} \)

\(\begin{cases}  3x \ge -15, / :3 \\ 3x\le 1 / : 3 \end{cases} \)

\(\begin{cases} x \ge -5, \\ x\le \frac13 \end{cases} \)

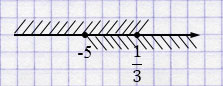
Ответ: \([-5; \frac13]\) , целые числа:

\(x=-5,\;-3,\;0\).

г) \(-2{,}5\le\dfrac{1-3y}{2}\le 1{,}5\)

\(\begin{cases} \dfrac{1-3y}{2} \ge -2,5,/\times 2 \\ \dfrac{1-3y}{2}\le 1,5 /\times 2 \end{cases}\)

\(\begin{cases} 1-3y \ge -5,\\ 1-3y\le 3 \end{cases}\)

\(\begin{cases} -3y \ge -5-1,\\ -3y\le 3-1 \end{cases}\)

\(\begin{cases} -3y \ge -6, / : (-3) \\ -3y\le 2 / : (-3)\end{cases} \)

\(\begin{cases} y \le 2, \\ y\ge -\frac23 \end{cases} \)

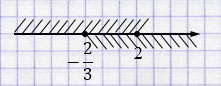
Ответ: \(\left[-\dfrac{2}{3},\,2\right]\), целые числа:

 \(0,\;1,\;2\).

Пояснения:

Двойное неравенство удобно раскладывать на систему из двух простых неравенств:

1) средняя часть больше левой части;

2) средняя часть меньше правой.

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

а) \(5^m \cdot 5^{m+1} \cdot 5^{1-m} = \)

\(=5^{m + (m + 1) + (1 - m)}=\)

\(=5^{m + \cancel m + 1 + 1 - \cancel m}= 5^{m+2}\).

б) \((5^m)^2 \cdot (5^{-3})^m = 5^{2m} \cdot 5^{-3m} =\)

\(=5^{2m +(-3m)} = 5^{-m}.\)

в) \(625 : 5^{4m-2}=5^4 : 5^{4m-2} = \)

\(=5^{4 - (4m - 2)} =5^{4 - 4m + 2} = 5^{6 - 4m}.\)

Пояснения:

Свойства степеней:

\( a^m \cdot a^n = a^{m+n}, \)

\(\frac{a^m}{a^n} = a^{m-n}, \)

\((a^m)^n = a^{m \cdot n}. \)