Упражнение 1061 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

Пусть \(x\) км туристы проходят в день сейчас. Если они будут идти на 5 км больше, то за 6 дней пройдут \(6(x + 5)\) км, и это больше 90 км. Если они будут идти на 5 км меньше, то за 8 дней пройдут \(8(x - 5)\) км, и это меньше 90 км:

Составим систему неравенств:

\(\begin{cases} 6(x + 5) > 90,\\ 8(x - 5) < 90 \end{cases} \)

\(\begin{cases} 6x + 30 > 90,\\ 8x - 40 < 90 \end{cases} \)

\(\begin{cases} 6x > 90 - 30,\\ 8x < 90 + 40 \end{cases} \)

\(\begin{cases} 6x > 60,  / : 6 \\ 8x <130  / : 8 \end{cases} \)

\(\begin{cases} x > 10, \\ x <\frac{130}{8} \end{cases} \)

\(\begin{cases} x > 10, \\ x <\frac{65}{4} \end{cases} \)

\(\begin{cases} x > 10, \\ x < 16,25 \end{cases} \)

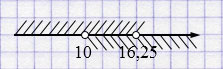
\(x \in (10; 16,25)\).

Ответ: в день туристы проходят более \(10\) км, но менее \(16,25\) км.

Пояснения:

Обозначив расстояние, которое туристы проходят в день сейчас за \(x\) км. Составляем систему из двух неравенств, учитывая то, что при увеличении дневного пути на 5 км, общее пройденное расстояние, равное \(6(x + 5)\), становится больше 90 км. А при уменьшении дневного пути на 5 км, общее пройденное расстояние, равное \(8(x - 5)\), становится меньше 90 км.

При решении системы неравенств используем то, что

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

а) \(0{,}987^{-1} > 1\)

\(0{,}987^{-1}=\left(\dfrac{987}{1000}\right)^{-1}=\)

\(=\dfrac{1000}{987} = 1\dfrac{13}{987} > 1 \).

б) \(1{,}074^{-1} < 1\)

\(1{,}074^{-1}=\left(\dfrac{1074}{1000}\right)^{-1}=\)

\(=\dfrac{1000}{1074} < 1\)

Пояснения:

Если \(\displaystyle A\neq 0\), то \(A^{-1}=\dfrac{1}{A}\).

Любая неправильная дробь (числитель больше знаменателя) всегда больше единицы.

Любая правильная дробь (числитель меньше знаменателя) всегда меньше единицы.