Упражнение 1057 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(\begin{cases} 3(y-1)-4(y+8)<5(y+5), \\[2pt]1{,}2(1+5y)-0{,}2<5(1-3y)-3y \end{cases} \)

\(\begin{cases} 3y-3-4y-32<5y+25, \\[2pt]1{,}2+6y-0{,}2<5-15y-3y \end{cases} \)

\(\begin{cases} -y-35<5y+25, \\[2pt]1+6y<5-18y \end{cases} \)

\(\begin{cases} -y-5y<25 + 35, \\[2pt] 6y + 18y<5 - 1 \end{cases} \)

\(\begin{cases} -6y<60,  / : (-6) \\[2pt] 24y<4  / : 24 \end{cases} \)

\(\begin{cases} y>-10, \\[2pt] y<\frac{4}{24} \end{cases} \)

\(\begin{cases} y>-10, \\[2pt] y<\frac{1}{6} \end{cases} \)

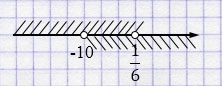
\(y \in (-10; \frac16)\)

Ответ: положительные значения при \(y \in(0; \frac16)\).

б) \(\begin{cases} 15(y-4) - 14(y - 3) < y(y-9) - y^2, \\[4pt] \dfrac{5-y}{3} - y > 14 - \dfrac{2-y}{6}   /\times6 \end{cases} \)

\(\begin{cases} 15y-60 - 14y + 42 < \cancel{y^2}-9y - \cancel{y^2}, \\[4pt] 2(5-y) - 6y > 84 - (2-y) \end{cases} \)

\(\begin{cases} y-18 < -9y, \\[4pt] 10-2y - 6y > 84 - 2+y \end{cases} \)

\(\begin{cases} y+9y < 18, \\[4pt] 10-8y > 82+y \end{cases} \)

\(\begin{cases} 10y < 18,  / : 10 \\[4pt] -8y - y > 82 - 10 \end{cases} \)

\(\begin{cases} y < \frac{18}{10}, \\[4pt] -9y > 72   / : (-9) \end{cases} \)

\(\begin{cases} y < 1,8, \\[4pt] y < -8 \end{cases} \)

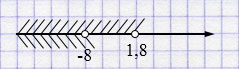
\(y \in (-\infty; -8)\)

Ответ: положительныч значений \(y\) нет.

в) \(\begin{cases} (2y-1)(3y+2)-6y(y-4)<48, \\[4pt] \dfrac{y-1}{8}-\dfrac{6y+1}{4}-1<0 /\times8 \end{cases} \)

\(\begin{cases} \cancel{6y^2} + 4y -3y - 2- \cancel{6y^2}+24y<48, \\[4pt] y-1-2(6y+1)-8<0 \end{cases} \)

\(\begin{cases} 25y - 2<48, \\[4pt] y-1-12y-2-8<0 \end{cases} \)

\(\begin{cases} 25y <48 + 2, \\[4pt] -11y- 11<0 \end{cases} \)

\(\begin{cases} 25y <50,  / : 25 \\[4pt] -11y < 11  / : (-11) \end{cases} \)

\(\begin{cases} y < 2, \\[4pt] y > -1 \end{cases} \)

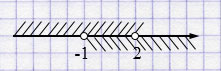
\(y \in(-1; 2)\)

Ответ: положительные значения при \(y \in (0; 2)\).

Пояснения:

Чтобы найти положительные значения \(y\), удовлетворяющие системе неравенств, нужно решить эту систему и из решения системы выбрать положительные значения \(y\).

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении систем неравенств, сначала, если необходимо, избавляемся от знаменателей, домножив обе части неравенства на общий знаменатель всех дробей, входящих в него, затем раскрываем скобки, используя распределительное свойство умножения, при этом используем свойства неравенств:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

а) \(\left(\dfrac{a+1}{a^{2}+1-2a}+\dfrac{1}{a-1}\right)\cdot\left(\dfrac{a}{a-1}\right)^{-1}-\dfrac{2}{a-1}=0\)

\(\left(\dfrac{a+1}{(a-1)^2}+\dfrac{1}{a-1} ^{\color{blue}{\backslash a-1}}  \right)\cdot\dfrac{a-1}{a}-\dfrac{2}{a-1}=0\)

\(\dfrac{a+\cancel1 + a - \cancel1}{(a-1)^2}\cdot\dfrac{a-1}{a}-\dfrac{2}{a-1}=0\)

\(\dfrac{2\cancel a}{(a-1)^{\cancel2}}\cdot\dfrac{\cancel{a-1}}{\cancel a}-\dfrac{2}{a-1}=0\)

\(\dfrac{2}{a-1}-\dfrac{2}{a-1}=0\)

\(0=0\)

б) В учебнике допущена опечатка, чтобы тождество было доказуемо в первых скобках в числителе второй дроби выражение \(1-y\) заменяем на выражение \(y-1\).

\(\left(\dfrac{1+x}{x^{2}-xy}+\dfrac{y-1}{y^{2}-xy}\right)\cdot\left(\dfrac{x+y}{x^{2}y-y^{2}x}\right)^{-1}=1\)

\(\left(\dfrac{1+x}{x(x-y)}+\dfrac{y-1}{-y(x-y)}\right)\cdot\dfrac{x^{2}y-y^{2}x}{x+y}=1\)

\(\left(\dfrac{1+x}{x(x-y)} ^{\color{blue}{\backslash y}} -\dfrac{y-1}{y(x-y)} ^{\color{blue}{\backslash x}} \right)\cdot\dfrac{xy(x-y)}{x+y}=1\)

\(\dfrac{y(1+x)-x(y-1)}{x(x-y)}\cdot\dfrac{xy(x-y)}{x+y}=1\)

\(\dfrac{y+\cancel{xy}-\cancel{xy}+x}{\cancel{xy}\cancel{(x-y)}}\cdot\dfrac{\cancel{xy}\cancel{(x-y)}}{x+y}=1\)

\(\dfrac{y+x}{x+y}=1\)

\(1 = 1\)

в) \(3a\left(\dfrac{1}{a-c}-\dfrac{c}{a^{3}-c^{3}}\cdot\dfrac{a^{2}+c^{2}+ac}{a+c}\right)-\left(\dfrac{a^{2}-c^{2}}{3c^{2}}\right)^{-1}=3\)

\(3a\left(\dfrac{1}{a-c}-\dfrac{c}{(a-c)\cancel{(a^{2}+ac+c^{2})}}\cdot\dfrac{\cancel{a^{2}+ac+c^{2}}}{a+c}\right)-\dfrac{3c^{2}}{a^{2}-c^{2}}=3\)

\(3a\left(\dfrac{1}{a-c} ^{\color{blue}{\backslash a+c}} -\dfrac{c}{(a-c)(a+c)}\right)-\dfrac{3c^{2}}{a^{2}-c^{2}}=3\)

\(3a\cdot\dfrac{a+\cancel c-\cancel c}{(a-c)(a+c)}-\dfrac{3c^{2}}{a^{2}-c^{2}}=3\)

\(\dfrac{3a^2}{a^2-c^2}-\dfrac{3c^{2}}{a^{2}-c^{2}}=3\)

\(\dfrac{3a^2-3c^2}{a^2-c^2}=3\)

\(\dfrac{3\cancel{(a^2-c^2)}}{\cancel{a^2-c^2}}=3\)

\(3=3\)

Пояснения:

Обозначение степени \(-1\).

Если \(\displaystyle A\neq 0\), то \(A^{-1}=\dfrac{1}{A}\).

Сокращение дробей и разложение на множители.

Во всех пунктах важно раскладывать многочлены на множители:

\( a^{2}+1-2a=(a-1)^{2},\)

\(x^{2}-xy=x(x-y),\)

\(y^{2}-xy=y(y-x), \)

\( x^{2}y-y^{2}x=xy(x-y),\)

\(a^{3}-c^{3}=(a-c)(a^{2}+ac+c^{2}),\)

\(a^{2}-c^{2}=(a-c)(a+c). \)

Это позволяет сокращать одинаковые множители в числителе и знаменателе.

Пояснение к пункту а).

Сначала мы упрощаем сумму дробей, приведя их к общему знаменателю \((a-1)^{2}\). Затем пользуемся тем, что степень \(-1\) даёт обратную дробь. После сокращения получаем две одинаковые дроби \(\dfrac{2}{a-1}\), которые при вычитании дают 0.

Пояснение к пункту б).

Сначала приводим две дроби к общему знаменателю \(xy(x-y)\). Важно аккуратно работать со знаками при переходе от \(y^{2}-xy\) к \(y(y-x)\). После приведения к общему знаменателю числитель сводится к \(x+y\), так что вся скобка равна \(\dfrac{x+y}{xy(x-y)}\). Вторая скобка с степенью \(-1\) даёт обратную дробь \(\dfrac{xy(x-y)}{x+y}\); произведение взаимно обратных дробей равно 1.

Если в учебнике в числителе второй дроби напечатано \(1-y\), то это опечатка: при числителе \(y-1\) тождество действительно выполняется.

Пояснение к пункту в).

Главный приём — разложить \(a^{3}-c^{3}\) на множители и сократить множитель \(a^{2}+ac+c^{2}\). После этого в скобке остаются две дроби с одинаковым знаменателем \(a^{2}-c^{2}\), и их разность легко упрощается до \(\dfrac{a}{a^{2}-c^{2}}\). Далее умножение на \(3a\) даёт \(\dfrac{3a^{2}}{a^{2}-c^{2}}\). Последняя дробь со степенью \(-1\) превращается в \(\dfrac{3c^{2}}{a^{2}-c^{2}}\), и вычитание даёт \(\dfrac{3(a^{2}-c^{2})}{a^{2}-c^{2}}=3\).

Во всех трёх пунктах тождества доказаны с помощью одинаковых приёмов: разложения на множители, приведения к общему знаменателю и использования взаимно обратных дробей.