Упражнение 19 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 10

а) \(x < 3\)

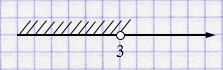
\(x \in (-\infty; 3)\)

б) \(-2 < x < 4\)

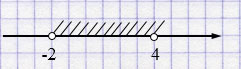
\(x \in(-2; 4)\)

в) \(x \ge 1\)

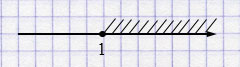
\(x\in[1; +\infty)\)

г) \(5 \le x \le 7{,}5\)

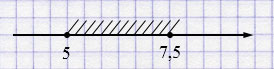
\(x\in[5; 7{,}5]\)

д) \(0 < x \le 2{,}5\)

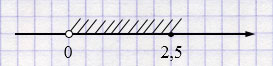
\(x\in(0; 2{,}5]\)

е) \(x \ge 10{,}5\)

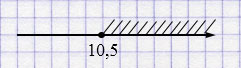
\(x\in[10{,}5; +\infty)\)

Пояснения:

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.