Упражнение 112 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

а) \(y = -3x + 1\)

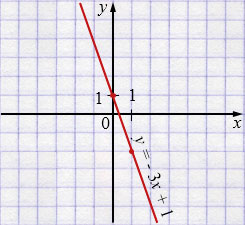
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(y = 0\) при \(x = \frac13\).

4. \(y > 0\) при \(x < \frac13\),

\(y < 0\) при \(x > \frac13\).

5. Функция убывает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

б) \(y = 5 + 2x\)

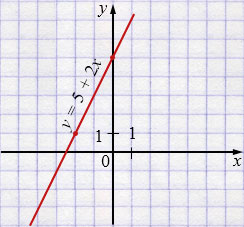
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(y = 0\) при \(x = -2,5\).

4. \(y > 0\) при \(x > -2,5\),

\(y < 0\) при \(x < -2,5\).

5. Функция возрастает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

в) \(y =-\frac3x;\)

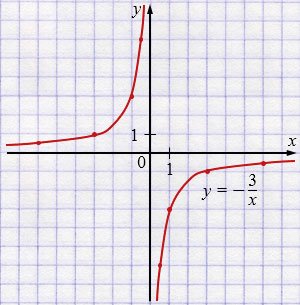
Свойства:

1. \(D(f) = (-\infty; 0) \cup (0; + \infty)\).

2. \(E(f) = (-\infty; 0) \cup (0; + \infty)\).

3. Нули функции не существуют.

4. \(y > 0\) при \(x < 0\),

\(y < 0\) при \(x > 0\).

5. Функция возрастает на \((-\infty; 0)\) и \((0; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция является нечетной.

г) \(y = \frac{1}{2x}\)

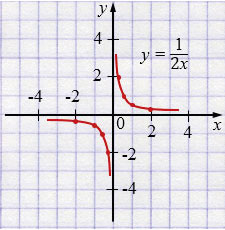
Свойства:

1. \(D(f) = (-\infty; 0) \cup (0; + \infty)\).

2. \(E(f) = (-\infty; 0) \cup (0; + \infty)\).

3. Нули функции не существуют.

4. \(y > 0\) при \(x > 0\),

\(y < 0\) при \(x < 0\).

5. Функция убывает на \((-\infty; 0)\) и \((0; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция не является ни четной и ни нечетной.

д) \(y = -x^2\)

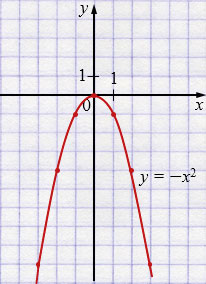
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; 0]\).

3. \(y = 0\) при \(x = 0\).

4. \(y < 0\) при \(x \ne 0\).

5. Функция возрастает на \((-\infty;0]\) и убывает на \([0; + \infty)\).

6. Наибольшее значение функции равно нулю при \(x = 0\).

7. Функция является четной.

е) \(y = -x^3\)

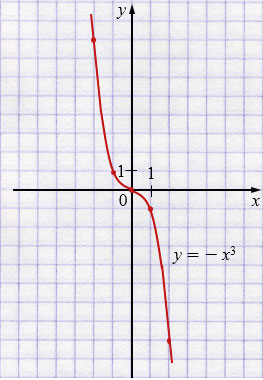
Свойства:

1. \(D(f) = (-\infty; + \infty)\).

2. \(E(f) = (-\infty; + \infty)\).

3. \(y = 0\) при \(x =0\).

4. \(y > 0\) при \(x < 0\),

\(y < 0\) при \(x > 0\).

5. Функция убывает на \((-\infty; + \infty)\).

6. Наибольшего и наименьшего значений функция не имеет.

7. Функция является нечетной.

Пояснения:

Основные свойства функций:

1. Область определения \(D(f)\).

2. Множество значений \(E(f)\).

3. Нули функции - значения аргумента (\(x\)), при которых функция (\(y\)) обращается в нуль.

4. Промежутки знакопостоянства - промежутки, на которых функция сохраняет знак (на промежутках, расположенных выше оси \(x\) функция принимает положительные значения, на промежутках, расположенных ниже оси \(x\) функция принимает отрицательные значения).

5. Промежутки монотонности функции - промежутки возрастания и убывания функции. Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то - убывающей функцией.

6. Наибольшее и наименьшее значения функции, если существуют.

7. Четность/нечетность функции.

Функция называется четной, если выполняются следующие условия:

- область определения функции симметрична относительно оси ординат (оси \(y\));

- противоположным значениям аргумента соответствуют равные значения функции.

Функция называется нечетной, если выполняются следующие условия:

- область определения функции симметрична относительно начала координат;

- противоположным значениям аргумента соответствуют противоположные значения функции.

\( y = x^{2}\)

а) \( y = (x - 2)^{2} + 3 \)

б) \( y = -(x - 3)^{2} + 5 \)

Пояснения:

1. Общий вид параболы

\[ y = (x - a)^{2} + b \]

Вершина имеет координаты \((a; b)\). Если \(a>0\) — сдвиг вправо, если \(a<0\) — влево. Если \(b>0\) — сдвиг вверх, если \(b<0\) — вниз.

а) Графиком функции \( y = (x - 2)^{2} + 3\) является парабола \(y = x^{2}\), смещённая вверх на 3 единицы и вправо на 2 единицы. Вершина: \((2; 3)\). Ветви направлены вверх. 

б) Графиком функции \(y = -(x - 3)^{2} + 5\) является парабола \(y = x^{2}\), отражённая относительно оси \(Ox\) и сдвинутая вверх на 5 единиц и вправо на 3 единицы. Вершина: \((3; 5)\). Ветви направлены вниз.