Упражнение 141 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 55
Вернуться к содержанию учебника
Вопрос
С помощью шаблона параболы \(y = x^{2}\) постройте график функции:
а) \(y = (x + 3)^{2} - 4\);
б) \(y = -(x + 4)^{2} - 2\).
Подсказка
Вспомните:
- Квадратичную функцию и ее график.
- Расположение точек на координатной плоскости.
Ответ
\( y = x^{2}\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
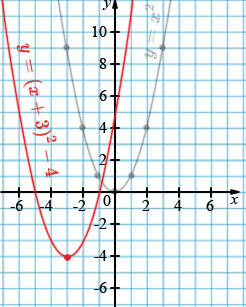
а) \( y = (x + 3)^{2} - 4 \)
б) \( y = -(x + 4)^{2} - 2 \)
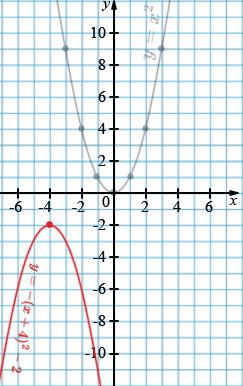
Пояснения:
1. Общий вид параболы
\[ y = (x - a)^{2} + b \]
Вершина имеет координаты \((a; b)\). Если \(a>0\) — сдвиг вправо, если \(a<0\) — влево. Если \(b>0\) — сдвиг вверх, если \(b<0\) — вниз.
а) Графиком функции \( y = (x + 3)^{2} - 4\) является парабола \(y = x^{2}\), смещённая вниз на 4 единицы и влево на 3 единицы. Вершина: \((-3; -4)\). Ветви направлены вверх.
б) Графиком функции \(y = -(x + 4)^{2} - 2\) является парабола \(y = x^{2}\), отражённая относительно оси \(Ox\) и сдвинутая вниз на 2 единицы и влево на 4 единицы. Вершина: \((-4; -2)\). Ветви направлены вниз.
Вернуться к содержанию учебника