Упражнение 452 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

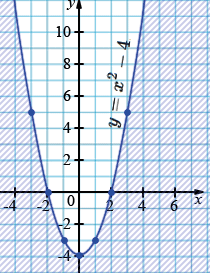
а) \(y \le x^2 - 4\);

\(y = x^2 - 4\)

Графиком данной функции является парабола, ветви которой направлены вверх, с вершиной в точке \((0; -4)\)

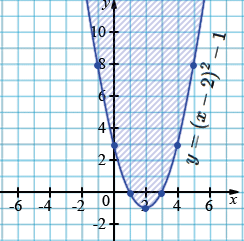
б) \(y \ge (x - 2)^2 - 1\)

\(y=(x - 2)^2 - 1\)

Графиком данной функции является парабола, ветви которой направлены вверх, с вершиной в точке \((2; -1)\)

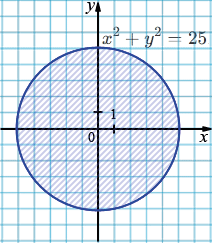
в) \(x^2 + y^2 \le 25\);

\(x^2 + y^2 = 25\) 

Графиком данного уравнения является окружность с центром в точке \((0; 0)\) и радиусом равным \(5.\)

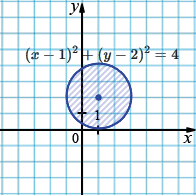
г) \((x - 1)^2 + (y - 2)^2 \le 4\).

\((x - 1)^2 + (y - 2)^2 = 4\)

Графиком данного уравнения является окружность с центром в точке \((1; 2)\) и радиусом равным \(2.\)

Пояснения:

Основные правила, используемые при решении:

1) Уравнение вида \(y = ax^2 + bx + c\) задаёт параболу. Неравенства вида \(y \le f(x)\) или \(y \ge f(x)\), где \(f(x)\) — квадратный трёхчлен, задают полуплоскость относительно параболы: ниже графика (\(\le\)) или выше (\(\ge\)).

2) Уравнение вида \((x - x_0)^2 + (y - y_0)^2 = R^2\) задаёт окружность с центром в точке \((x_0; y_0)\) и радиусом \(R\). Неравенства \((x - x_0)^2 + (y - y_0)^2 < R^2\) и \(\le R^2\) задают соответственно внутренность окружности без границы и с границей.

Пояснение к пункту а)

Функция \(y = x^2 - 4\) — парабола, ветви направлены вверх, вершина в точке \((0; -4)\). Неравенство \(y \le x^2 - 4\) означает, что для каждой точки \((x; y)\) её координата \(y\) не больше значения параболы. Поэтому штрихуется область под графиком параболы, включая саму линию.

Пояснение к пункту б)

График \(y = (x - 2)^2 - 1\) — парабола, полученная переносом стандартной параболы \(y = x^2\) на 2 единицы вправо и 1 единицу вниз. Её вершина в точке \((2; -1)\), ветви также вверх.

Неравенство \(y \ge (x - 2)^2 - 1\) задаёт все точки, у которых \(y\) не меньше значения параболы, то есть область над параболой, включая её.

Пояснение к пункту в)

Выражение \(x^2 + y^2\) — это квадрат расстояния от точки \((x; y)\) до начала координат \((0; 0)\). Уравнение

\[x^2 + y^2 = 25\]

описывает окружность с центром \((0; 0)\) и радиусом \(R = 5\), так как \(R^2 = 25\).

Неравенство \(x^2 + y^2 < 25\) означает, что квадрат расстояния меньше \(25\), то есть расстояние от точки до начала координат меньше \(5\). Значит, это все точки внутри окружности радиуса \(5\), но сама окружность не входит (строгий знак).

Пояснение к пункту г)

Запишем окружность:

\[(x - 1)^2 + (y - 2)^2 = 4.\]

Центр окружности \((1; 2)\), радиус \(R = 2\), так как \(R^2 = 4\).

Неравенство \((x - 1)^2 + (y - 2)^2 \le 4\) говорит, что расстояние от точки \((x; y)\) до центра \((1; 2)\) не превосходит \(2\). Значит, на координатной плоскости нужно изобразить круг радиуса \(2\) с центром \((1; 2)\) вместе с границей (окружностью).

Итак, для каждого пункта строим соответствующую параболу или окружность как границу и затем отмечаем нужную часть плоскости: ниже/выше параболы или внутри круга.

а) \( \begin{cases} y=x^3, \\ y = 15x \end{cases} \)

\( y=x^3\) - кубическая парабола, I и III четверть.

\(y = 15x\) - возрастающая прямая, проходит через точку \((0;0)\).

Ответ: система имеет 3 решения.

б) \( \begin{cases} xy=10, \\ y = x \end{cases} \)

\( \begin{cases} y=\frac{10}{x}, \\ y = x \end{cases} \)

\(y=\frac{10}{x}\) - гипербола, I и III четверть.

\(y=x\) - возрастающая прямая, проходит через точку \((0;0)\).

Ответ: система имеет 2 решения.

в) \(\begin{cases} x^2 + y^2 =36, \\ y=x^2 + 3 \end{cases}\)

\(x^2 + y^2 =36\) - окружность с центром \((0;0)\) и радиусом \(r = 6\).

\(y = x^2 + 3\) - парабола с вершиной в точке \((0; 3)\), ветви вверх.

Ответ: система имеет 2 решения.

Пояснения:

Суть графического метода решения системы уравнений с двумя переменными:

1) построить на одной координатной плоскости графики уравнений, входящих в систему;

2) найти координаты всех точек пересечения построенных графиков;

3) полученные пары чисел и будут искомыми решениями.

а) График \(y=x^3\) — кубическая парабола, а \(y=15x\) — прямая через начало координат. Они пересекаются в трёх точках, что соответствует трём решениям.

б) График \(xy=10\) — гипербола, а \(y=x\) — прямая, которая является биссектрисой угла между осями. Они пересекаются в двух точках, что соответствует двум решениям.

в) График \(x^2 + y^2 =36\) — окружность с центром \((0;0)\) и радиусом \(r = 6\), а \(y = x^2 + 3\) - парабола с вершиной в точке \((0; 3)\), ветви вверх. Они пересекаются в двух точках, что соответствует двум решениям.