Упражнение 453 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 134
Вернуться к содержанию учебника
Вопрос
(Для работы в парах.) Изобразите на координатной плоскости множество решений неравенства:
а) \(xy < 4\); б) \(xy > -6\).
1) Разберите совместно пример 3, приведённый в пункте 23.
2) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.
3) Проверьте друг у друга правильность выполнения задания и исправьте ошибки, если они допущены.
Подсказка
Ответ
а) \(xy < 4\)
\[y < \frac{4}{x}, \quad x \ne 0.\]
Граница множества решений — гипербола
\(y = \frac{4}{x}\)
| \(x\) | 0,5 | 1 | 2 | 4 | 8 | -0,5 | -1 | -2 | -4 | -8 |
| \(y\) | 8 | 4 | 2 | 1 | 0,5 | -8 | -4 | -2 | -1 | -0,5 |
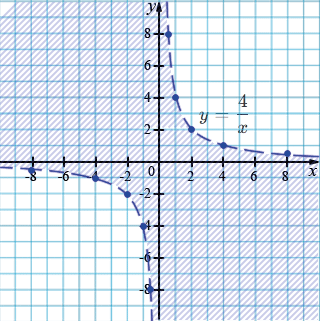
\((2; 4):\) \(2\cdot4 < 4\) - неверно.
\((0; -2):\) \(0\cdot(-2) < 4\) - верно.
\((-2; -4):\) \((-2)\cdot(-4) < 4\) - неверно.
б) \(xy > -6\)
Граница множества решений — гипербола
\(y = -\frac{6}{x}\)
| \(x\) | 1 | 2 | 3 | 6 | -1 | -2 | -3 | -6 |
| \(y\) | -6 | -3 | -2 | -1 | 6 | 3 | 2 | 1 |
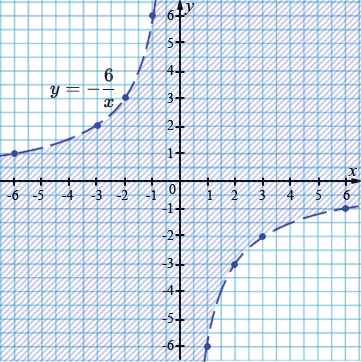
\((-3; 4):\) \(-3\cdot4 >-6\) - неверно.
\((1; 1):\) \(1\cdot1 >-6\) - верно.
\((4; -4):\) \(4\cdot(-4) >-6\) - неверно.
Пояснения:
1. Общий вид неравенств:
Если дано неравенство вида \(xy \,\square\, k\) (где \(\square\) — знак \(<\) или \(>\)), то удобно выразить одну переменную через другую:
\[xy \,\square\, k \;\Longrightarrow\; y \,\square\, \frac{k}{x}, \quad x \ne 0.\]
Это означает, что границей множества решений является гипербола \(y = \dfrac{k}{x}\), а сами решения — точки, лежащие выше или ниже этой гиперболы.
2. Гипербола делит плоскость на три части, чтобы понять, какую из них заштриховать надо подставить координаты любой точки из каждой области и проверить обращается ли неравенство в верное.
Знак строгий (\(<\) или \(\ > \)) — границу рисуем штриховой и не включаем её в решение; знак нестрогий (\(\le\), \(\ge\)) — границу рисуем сплошной и включаем.
Вернуться к содержанию учебника